Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Given the substitutions
ln 2=a,ln 3=b, and
ln 5=c, find the value of
ln((e)/(3)) in terms of
a,b, and
c.
Answer:

Given the substitutions $\ln 2=a, \ln 3=b$ , and $\ln 5=c$ , find the value of $\ln \left(\frac{e}{3}\right)$ in terms of $a, b$ , and $c$ . $\newline$ Answer:

View step-by-step help

View step-by-step help

Write and solve direct variation equations

Full solution

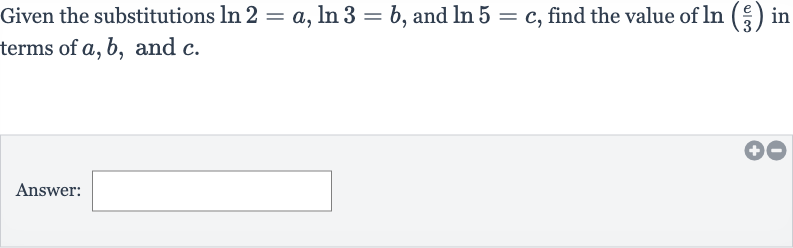
Q. Given the substitutions

\ln 2=a, \ln 3=b

, and

\ln 5=c

, find the value of

\ln \left(\frac{e}{3}\right)

in terms of

a, b

, and

c

.

\newline

Answer:

Express $\ln\left(\frac{e}{3}\right)$ : Express $\ln\left(\frac{e}{3}\right)$ using the properties of logarithms. $\newline$ We know that $\ln(e) = 1$ because the natural logarithm of $e$ to the power of $1$ is $e$ . We also know that $\ln(3) = b$ . Using the quotient rule for logarithms, which states that $\ln\left(\frac{x}{y}\right) = \ln(x) - \ln(y)$ , we can write $\ln\left(\frac{e}{3}\right)$ as $\ln(e) - \ln(3)$ .
Substitute known values: Substitute the known values into the expression. $\newline$ Substitute $\ln(e) = 1$ and $\ln(3) = b$ into the expression from Step $1$ . $\newline$ $\ln\left(\frac{e}{3}\right) = \ln(e) - \ln(3) = 1 - b$
Simplify expression: Simplify the expression. $\newline$ Simplify the expression to get the final answer in terms of $a$ , $b$ , and $c$ . $\newline$ $\ln\left(\frac{e}{3}\right) = 1 - b$ $\newline$ Since there are no terms involving $a$ or $c$ , the expression remains as is.

More problems from Write and solve direct variation equations

Question

In a direct variation,

y=15

x=5

. Write a direct variation equation that shows the relationship between

x

y

. Write your answer as an equation with

y

first, followed by an equals sign.

Posted 2 months ago

Question

In an inverse variation,

y = 4

x = 6

. Write an inverse variation equation that shows the relationship between

x

y

. Write the equation using a decimal or an integer.

\_\_\_\_

Posted 2 months ago

Question

z

varies directly with

y

and inversely with

x

y = -12

x = -4

z = -36

. What is the equation of variation? Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions. Remember to include the value of

k

, the constant of variation, in exact form.

\newline

\ z

Posted 2 months ago

Question

Which equation describes this relationship? Remember to include

k

, the constant of variation.

a

varies directly with

b

and inversely with

c

d

\newline

\newline

\[[A]a = \frac{kb}{cd}\]

\newline

\[[B]a = \frac{kbd}{c}\]

\newline

\[[C]a = \frac{k}{bcd}\]

\newline

\[[D]a = \frac{kd}{bc}\]

Posted 2 months ago

Question

z

varies directly with

y

and inversely with

w

x

y = 12

w = 8

x = –5

z = –3

. What is the value of

k

, the constant of variation?

\newline

Write your answer in the form

A

\frac {(A)}{(B)}

A

B

are constants or variable expressions.

\newline

Posted 2 months ago

Question

Square VWXY is dilated by a scale factor of

6

V^{\prime} W^{\prime} X^{\prime} Y^{\prime}

. Side W'X' measures

12

. What is the measure of side WX?

\newline

Posted 2 months ago

Question

6

2

\newline

2

4

2

11

1

2

16

2

\newline

In the system of equations, r is a constant. For what value of r does the system of linear equations have infinitely many solutions?

Posted 2 months ago

Question

1

5

\newline

Use the given information to find

m \angle P Q W

\newline

2

\newline

m \angle P Q W

m \angle W Q R=134 x

m \angle P Q R=169^{\circ}

m \angle P Q W=36 x-1

Posted 2 months ago

Question

10+7 x=4 x+2+b x

\newline

In the equation shown,

b

is a constant. For what value of

b

does the equation have no solutions?

\newline

1

\newline

3

\newline

5

\newline

6

\newline

7

Posted 2 months ago

Question

Graph the function

f(x)=x^{2}+4 x+5

\newline

Plot the vertex. Then plot another point on the parabola. If you make a mistake, you can erase your parabola by selecting the second point and placing it on top of the first.

\newline

\newline

\newline

\newline

\newline

100

Posted 5 hours ago