Resources

Testimonials

Plans

Resources

Testimonials

Plans

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

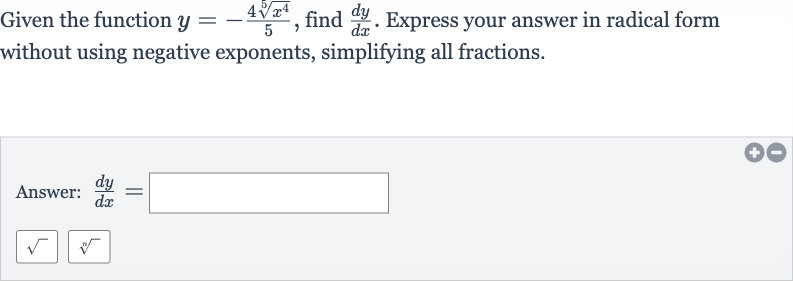
$Given the function y=-(4root(5)(x^(4)))/(5), find (dy)/(dx). Express your answer in radical form without using negative exponents, simplifying all fractions. Answer: (dy)/(dx)=$

Given the function $y=-\frac{4 \sqrt[5]{x^{4}}}{5}$ , find $\frac{d y}{d x}$ . Express your answer in radical form without using negative exponents, simplifying all fractions. $\newline$ Answer: $\frac{d y}{d x}=$

View step-by-step help

Home

Math Problems

Precalculus

Find trigonometric ratios using multiple identities

Full solution

Q. Given the function

y=-\frac{4 \sqrt[5]{x^{4}}}{5}

, find

\frac{d y}{d x}

. Express your answer in radical form without using negative exponents, simplifying all fractions.

\newline

Answer:

\frac{d y}{d x}=

Given function: We are given the function $y = -\frac{4\sqrt{5}(x^4)}{5}$ , and we need to find its derivative with respect to $x$ , denoted as $\frac{dy}{dx}$ . We will use the power rule for differentiation, which states that the derivative of $x^n$ with respect to $x$ is $n\cdot x^{n-1}$ .
Rewrite function: First, let's rewrite the function to make it easier to differentiate. The function is $y = -\frac{4\sqrt{5}(x^4)}{5}$ . We can pull out the constants and the radical to simplify the differentiation process. $\newline$ $y = -\frac{4}{5} \times \sqrt{5} \times x^4$
Apply power rule: Now, we apply the power rule to the $x^4$ term. The derivative of $x^4$ with respect to $x$ is $4\cdot x^{4-1}$ or $4\cdot x^3$ . $\newline$ $\frac{dy}{dx} = -\frac{4}{5} \cdot \sqrt{5} \cdot 4 \cdot x^3$
Simplify constants: Next, we simplify the expression by multiplying the constants together. $\frac{dy}{dx} = -\frac{16}{5} \times \sqrt{5} \times x^3$
Final expression: Finally, we express the answer in radical form without using negative exponents, simplifying all fractions. The expression is already in the correct form, so no further simplification is needed. $\frac{dy}{dx} = -\frac{16\sqrt{5}}{5} \cdot x^3$