AI tutor
Full solution
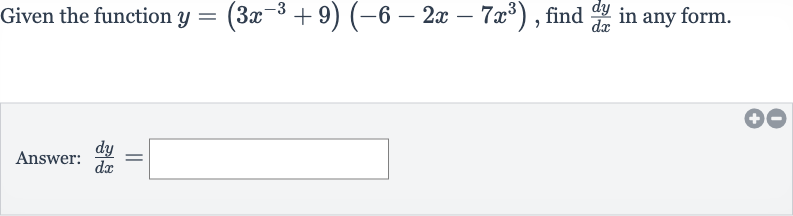
Q. Given the function , find in any form.Answer:
- Apply Product Rule: Apply the product rule to find the derivative of the product of two functions.The product rule states that , where and are functions of .Let and .
- Find : Find the derivative of with respect to .
- Find : Find the derivative of with respect to .
- Apply Product Rule with Derivatives: Apply the product rule using the derivatives and .
- Simplify Expression: Simplify the expression by distributing and combining like terms.
More problems from Transformations of quadratic functions
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help