Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Given the function
y=(2x^(3))/(2+x^(3)), find
(dy)/(dx) in simplified form.
Answer:
(dy)/(dx)=

Given the function $y=\frac{2 x^{3}}{2+x^{3}}$ , find $\frac{d y}{d x}$ in simplified form. $\newline$ Answer: $\frac{d y}{d x}=$

View step-by-step help

View step-by-step help

Write a formula for an arithmetic sequence

Full solution

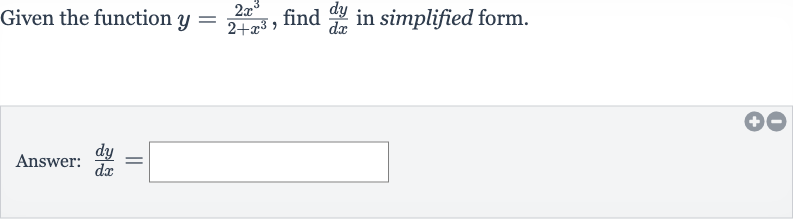
Q. Given the function

y=\frac{2 x^{3}}{2+x^{3}}

, find

\frac{d y}{d x}

in simplified form.

\newline

Answer:

\frac{d y}{d x}=

Identify Function: Identify the function that needs to be differentiated. $\newline$ The function given is $y=\frac{2x^{3}}{2+x^{3}}$ . We need to find the derivative of this function with respect to $x$ , which is denoted as $\frac{dy}{dx}$ .
Apply Quotient Rule: Apply the quotient rule for differentiation. The quotient rule states that if we have a function $y = \frac{u}{v}$ , where both $u$ and $v$ are functions of $x$ , then the derivative of $y$ with respect to $x$ is given by $\frac{dy}{dx} = \frac{v\frac{du}{dx} - u\frac{dv}{dx}}{v^2}$ . Here, $u = 2x^3$ and $v = 2 + x^3$ .
Differentiate $u$ and $v$ : Differentiate $u$ and $v$ with respect to $x$ . The derivative of $u = 2x^3$ with respect to $x$ is $\frac{du}{dx} = 6x^2$ . The derivative of $v = 2 + x^3$ with respect to $x$ is $v$ $0$ .
Substitute Derivatives: Substitute the derivatives into the quotient rule formula. $\newline$ Using the derivatives from Step $3$ , we substitute into the quotient rule formula: $\newline$ $\frac{dy}{dx} = \frac{(2 + x^3)(6x^2) - (2x^3)(3x^2)}{(2 + x^3)^2}$ .
Simplify Expression: Simplify the expression. $\newline$ $(\frac{dy}{dx}) = \frac{12x^2 + 6x^5 - 6x^5}{4 + 4x^3 + x^6}$ . $\newline$ This simplifies to $(\frac{dy}{dx}) = \frac{12x^2}{4 + 4x^3 + x^6}$ .
Factor Out Common Terms: Further simplify the expression by factoring out common terms if possible. $\newline$ We can factor out a $4$ from the numerator and denominator: $\newline$ $\frac{dy}{dx} = \frac{4 \times 3x^2}{4 \times (1 + x^3 + (\frac{1}{4})x^6)}$ . $\newline$ This simplifies to $\frac{dy}{dx} = \frac{3x^2}{1 + x^3 + (\frac{1}{4})x^6}$ .

More problems from Write a formula for an arithmetic sequence

Question

Find the sum of the finite arithmetic series.

\sum_{n=1}^{10} (7n+4)

\newline

Posted 2 months ago

Question

Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`

Posted 1 month ago

Question

Type the missing number in this sequence: `2, 4 8`, ______,`32`

Posted 2 months ago

Question

What kind of sequence is this?

2, 10, 50, 250, \ldots

Choices:Choices:

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 2 months ago

Question

What is the missing number in this pattern?

1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_

Posted 1 month ago

Question

Classify the series.

\sum_{n = 0}^{12} (n + 2)^3

\newline

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 1 month ago

Question

Find the first three partial sums of the series.

\newline

1 + 6 + 11 + 16 + 21 + 26 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 1 month ago

Question

Find the third partial sum of the series.

\newline

3 + 9 + 15 + 21 + 27 + 33 + \cdots

\newline

Write your answer as an integer or a fraction in simplest form.

\newline

S_3 =

Posted 1 month ago

Question

Find the first three partial sums of the series.

\newline

1 + 7 + 13 + 19 + 25 + 31 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 2 months ago

Question

Does the infinite geometric series converge or diverge?

\newline

1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots

\newline

\newline

\text{[A]converge}

\newline

\text{[B]diverge}

Posted 1 month ago