Resources

Testimonials

Plans

Resources

Testimonials

Plans

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

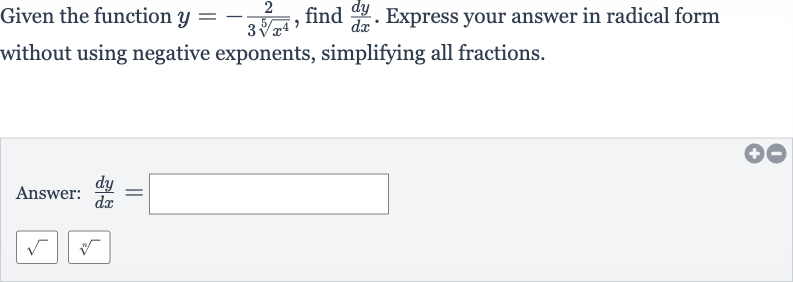
$Given the function y=-(2)/(3root(5)(x^(4))), find (dy)/(dx). Express your answer in radical form without using negative exponents, simplifying all fractions. Answer: (dy)/(dx)=$

Given the function $y=-\frac{2}{3 \sqrt[5]{x^{4}}}$ , find $\frac{d y}{d x}$ . Express your answer in radical form without using negative exponents, simplifying all fractions. $\newline$ Answer: $\frac{d y}{d x}=$

View step-by-step help

Home

Math Problems

Precalculus

Find trigonometric ratios using multiple identities

Full solution

Q. Given the function

y=-\frac{2}{3 \sqrt[5]{x^{4}}}

, find

\frac{d y}{d x}

. Express your answer in radical form without using negative exponents, simplifying all fractions.

\newline

Answer:

\frac{d y}{d x}=

Rewrite Function: We are given the function $y = -\frac{2}{3\sqrt{5}x^{4}}$ . To find the derivative $\frac{dy}{dx}$ , we will use the power rule for differentiation, which states that if $y = ax^n$ , then $\frac{dy}{dx} = n\cdot ax^{n-1}$ . In this case, we have a constant multiplied by $x$ raised to a power, so we will apply the power rule accordingly.
Apply Power Rule: First, let's rewrite the function to make it easier to differentiate. We can express the cube root of $5$ as $5^{1/3}$ and the variable $x$ to the power of $4$ as $x^4$ . So the function becomes $y = -\frac{2}{3\cdot 5^{1/3}\cdot x^4}$ . Now, we can treat $3\cdot 5^{1/3}$ as a constant coefficient and $x^4$ as the variable term.
Differentiate Variable Term: Applying the power rule, we differentiate the variable term $x^4$ . The derivative of $x^4$ with respect to $x$ is $4\cdot x^{4-1} = 4\cdot x^3$ . We will multiply this by the constant coefficient $-\frac{2}{3\cdot 5^{1/3}}$ .
Simplify Constants: The derivative of $y$ with respect to $x$ is then $\frac{dy}{dx} = -\frac{2}{3\cdot5^{\frac{1}{3}}} \cdot 4x^3$ . We can simplify this by multiplying the constants together.
Express Derivative: Multiplying the constants gives us $(dy)/(dx) = -\left(\frac{2 \cdot 4}{3 \cdot 5^{1/3}}\right) \cdot x^3 = -\left(\frac{8}{3 \cdot 5^{1/3}}\right) \cdot x^3$ . This is the derivative in terms of $x$ , but we need to express it without using negative exponents.
Check for Negative Exponents: Since there are no negative exponents in our expression, we do not need to make any further adjustments to the form of the derivative. The expression is already simplified, and the fraction is as simplified as it can be without a decimal approximation of the cube root of $5$ .
Final Derivative: Therefore, the derivative of the function $y = -\frac{2}{3\sqrt{5}x^{4}}$ with respect to $x$ is $\frac{dy}{dx} = -\left(\frac{8}{3\cdot 5^{1/3}}\right) \cdot x^3$ . This is the final answer in radical form, with all fractions simplified and no negative exponents.