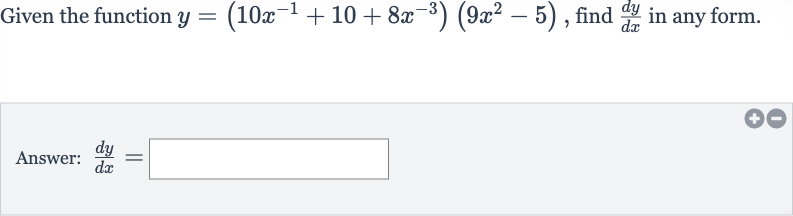
Given the function y=(10x^(-1)+10+8x^(-3))(9x^(2)-5), find (dy)/(dx) in any form. Answer: (dy)/(dx)=

Question

Given the function  y=(10x^(-1)+10+8x^(-3))(9x^(2)-5), find  (dy)/(dx) in any form. Answer:  (dy)/(dx)=

Bytelearn · Accepted Answer

Apply Product Rule: We are given the function y=(10x^(-1)+10+8x^(-3))(9x^(2)-5). To find the derivative dy/dx, we will use the product rule, which states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.Find Derivatives: Let's denote the first function as f(x) = 10x^(-1) + 10 + 8x^(-3) and the second function as g(x) = 9x^(2) - 5. We will first find the derivatives f'(x) and g'(x).Use Power Rule: The derivative of f(x) with respect to x is f'(x) = d/dx (10x^(-1) + 10 + 8x^(-3)). Using the power rule, we get f'(x) = -10x^(-2) - 24x^(-4).Apply Product Rule: The derivative of g(x) with respect to x is g'(x) = d/dx (9x^(2) - 5). Using the power rule, we get g'(x) = 18x.Simplify Expression: Now, we apply the product rule: (f(x)g(x))' = f'(x)g(x) + f(x)g'(x). Substituting the derivatives we found, we get (dy)/(dx) = (-10x^(-2) - 24x^(-4))(9x^(2) - 5) + (10x^(-1) + 10 + 8x^(-3))(18x).Combine Like Terms: We simplify the expression by multiplying the terms: (dy)/(dx) = (-90x^(-2) + 50x^(-2) - 216x^(-4) + 120x^(-4)) + (180x^(-1) + 180 + 144x^(-3)).Further Simplification: Combine like terms: (dy)/(dx) = (-40x^(-2) - 96x^(-4)) + (180x^(-1) + 180 + 144x^(-3)).Final Answer: Further simplification gives us: (dy)/(dx) = -40x^(-2) - 96x^(-4) + 180x^(-1) + 180 + 144x^(-3).We can write the final answer in a more simplified form by ordering the terms according to the powers of x: (dy)/(dx) = 180x^(-1) - 40x^(-2) + 144x^(-3) - 96x^(-4) + 180.

Given the function $y=\left(10 x^{-1}+10+8 x^{-3}\right)\left(9 x^{2}-5\right)$ , find $\frac{d y}{d x}$ in any form. $\newline$ Answer: $\frac{d y}{d x}=$

Full solution

More problems from Multiplication with rational exponents

Related topics

Given the function y=(10x−1+10+8x−3)(9x2−5) y=\left(10 x^{-1}+10+8 x^{-3}\right)\left(9 x^{2}-5\right) y=(10x−1+10+8x−3)(9x2−5), find dydx \frac{d y}{d x} dxdy​ in any form.\newlineAnswer: dydx= \frac{d y}{d x}= dxdy​=

Given the function $y=\left(10 x^{-1}+10+8 x^{-3}\right)\left(9 x^{2}-5\right)$ , find $\frac{d y}{d x}$ in any form. $\newline$ Answer: $\frac{d y}{d x}=$