Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

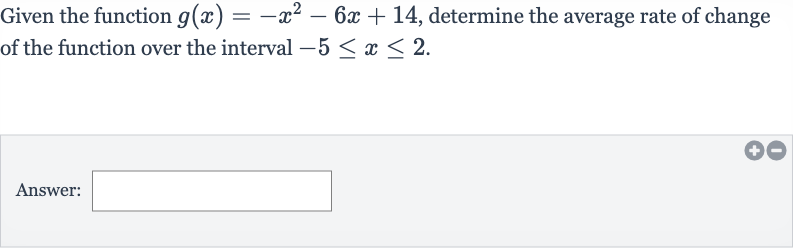
Given the function g(x)=-x^(2)-6x+14, determine the average rate of change of the function over the interval -5 <= x <= 2. Answer:

Given the function g(x)=−x2−6x+14 g(x)=-x^{2}-6 x+14 , determine the average rate of change of the function over the interval −5≤x≤2 -5 \leq x \leq 2 .\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Average rate of changeright chevron icon

Full solution

Q. Given the function g(x)=−x2−6x+14 g(x)=-x^{2}-6 x+14 , determine the average rate of change of the function over the interval −5≤x≤2 -5 \leq x \leq 2 .\newlineAnswer:
  1. Define Function: We have the function g(x)=−x2−6x+14g(x) = -x^2 - 6x + 14. To find the average rate of change over the interval [−5,2][-5, 2], we will use the formula for the average rate of change, which is (g(b)−g(a))/(b−a)(g(b) - g(a)) / (b - a), where aa and bb are the endpoints of the interval.
  2. Find g(−5)g(-5): First, we need to find the value of g(−5)g(-5). We substitute x=−5x = -5 into the function g(x)g(x).
    g(−5)=−(−5)2−6(−5)+14g(-5) = -(-5)^2 - 6(-5) + 14
    g(−5)=−(25)+30+14g(-5) = -(25) + 30 + 14
    g(−5)=−25+30+14g(-5) = -25 + 30 + 14
    g(−5)=5+14g(-5) = 5 + 14
    g(−5)=19g(-5) = 19
  3. Find g(2)g(2): Next, we need to find the value of g(2)g(2). We substitute x=2x = 2 into the function g(x)g(x).
    g(2)=−(2)2−6(2)+14g(2) = -(2)^2 - 6(2) + 14
    g(2)=−4−12+14g(2) = -4 - 12 + 14
    g(2)=−16+14g(2) = -16 + 14
    g(2)=−2g(2) = -2
  4. Calculate Average Rate of Change: Now we have the values g(−5)=19g(-5) = 19 and g(2)=−2g(2) = -2. We can calculate the average rate of change using the formula (g(b)−g(a))/(b−a)(g(b) - g(a)) / (b - a) with a=−5a = -5 and b=2b = 2.\newlineAverage rate of change = (g(2)−g(−5))/(2−(−5))(g(2) - g(-5)) / (2 - (-5))\newlineAverage rate of change = (−2−19)/(2−(−5))(-2 - 19) / (2 - (-5))\newlineAverage rate of change = (−21)/(7)(-21) / (7)\newlineAverage rate of change = −3-3

More problems from Average rate of change

Question
What is the domain of this function?\newline(9,–2)(6,–10)(–3,9)(5,2)(9,–2)(6,–10)(–3,9)(5,2)\newlineChoices:\newline(A){–3,5,6,9}(B){–10,–2,2,9}(C){2,5,6,9}(D){–6,–3,5,9}(A)\{–3,5,6,9\}\newline(B)\{–10,–2,2,9\}\newline(C)\{2,5,6,9\}\newline(D)\{–6,–3,5,9\}
Get tutor helpright-arrow

Posted 2 months ago

Question
Look at this set of ordered pairs:\newline(2,14)(2, 14)\newline(10,12)(10, 12)\newline(3,−19)(3, -19)\newlineIs this relation a function?\newlineChoices:\newline[[yes]\text{[[yes]}[no]]\text{[no]]}
Get tutor helpright-arrow

Posted 2 months ago

Question
Use the following function rule to find f(11) f(11) .\newlinef(x)=−10−7x f(x) = -10 - 7x \newlinef(11)= f(11) = _____
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the slope of the line y=−3x−25 y = -3x - \frac{2}{5} .\newlineSimplify your answer and write it as a proper fraction, improper fraction, or integer.\newline_____\_\_\_\_\_
Get tutor helpright-arrow

Posted 2 months ago

Question
A line has a slope of 33 and passes through the point (−2,−10)(-2,-10). Write its equation in slope-intercept form.\newlineWrite your answer using integers, proper fractions, and improper fractions in simplest form.
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the range of this function?\newliney = |x|\newlineChoices:\newlineall real numbers\text{all real numbers}\newline{y∣y≥0}\{y \mid y \geq 0\}\newline{y∣y≤0}\{y \mid y \leq 0\}\newline{y∣y>0}\{y \mid y > 0\}
Get tutor helpright-arrow

Posted 3 months ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 1 1 unit down of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the domain of this function?\newline(8,–1)(7,–11)(–4,10)(4,3)(8,–1)(7,–11)(–4,10)(4,3)\newlineChoices: \newline(A){–4,4,7,8}(A)\{–4,4,7,8\}\newline(B){–11,–1,3,10}(B)\{–11,–1,3,10\}\newline(C){3,4,7,8}(C)\{3,4,7,8\}\newline(D){–7,–4,4,8}(D)\{–7,–4,4,8\}
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the domain of this function?\newline(10, –3)(2, –9)(–5, 8)(3, 1)(10,\,–3)(2,\,–9)(–5,\,8)(3,\,1)\newlineChoices:\newline[{–5,2,3,10}][{–9, –3,1,8}][{1,2,3,10}][{–10, –5,2,3}][\{–5,2,3,10\}][\{–9,\,–3,1,8\}][\{1,2,3,10\}][\{–10,\,–5,2,3\}]
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the domain of this function?\newline(1,–4)(9,–12)(–6,11)(7,5)(1,–4)(9,–12)(–6,11)(7,5)\newlineChoices:(A){–6,1,7,9}\newline\\(A)\{–6,1,7,9\}\newline(B){–12,–4,5,11}(B)\{–12,–4,5,11\}\newline(C{5,1,7,9}(C\{5,1,7,9\}\newline(D){–9,–6,1,7}(D)\{–9,–6,1,7\}
Get tutor helpright-arrow

Posted 2 months ago

View all (25)