Full solution
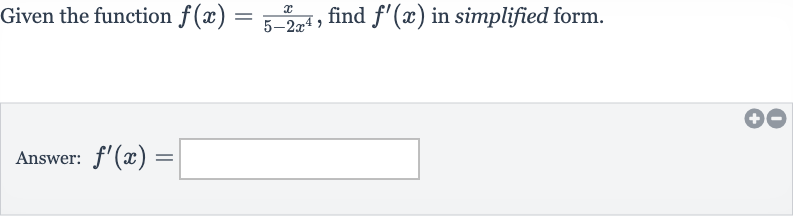
Q. Given the function , find in simplified form.Answer:
- Apply Quotient Rule: To find the derivative of the function , we will use the quotient rule. The quotient rule states that if we have a function that is the quotient of two functions, , then its derivative is given by:Here, and .
- Find : First, we find the derivative of with respect to . Since , the derivative is:
- Find : Next, we find the derivative of with respect to . Since , the derivative is:
- Apply Quotient Rule: Now we apply the quotient rule using the derivatives and we found:
- Simplify Numerator: Simplify the numerator of the derivative:
- Final Derivative: The derivative is now in simplified form:
More problems from Find the vertex of the transformed function
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help