Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Given the function
f(x)=(x)/(3-4x^(3)), find
f^(')(x) in simplified form.
Answer:
f^(')(x)=

Given the function $f(x)=\frac{x}{3-4 x^{3}}$ , find $f^{\prime}(x)$ in simplified form. $\newline$ Answer: $f^{\prime}(x)=$

View step-by-step help

View step-by-step help

Write a formula for an arithmetic sequence

Full solution

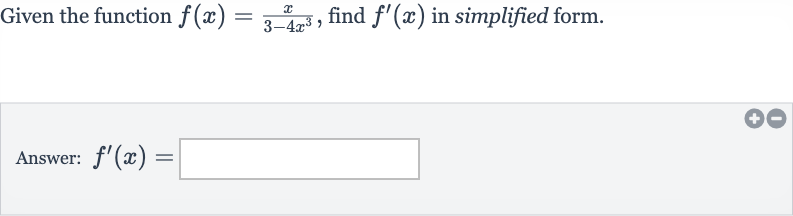
Q. Given the function

f(x)=\frac{x}{3-4 x^{3}}

, find

f^{\prime}(x)

in simplified form.

\newline

Answer:

f^{\prime}(x)=

Identify Function: Identify the function that needs to be differentiated. $\newline$ The function given is $f(x) = \frac{x}{3-4x^3}$ . We need to find its derivative, which is denoted by $f'(x)$ .
Apply Quotient Rule: Apply the quotient rule for differentiation. $\newline$ The quotient rule states that if we have a function that is the quotient of two functions, $\frac{u(x)}{v(x)}$ , then its derivative is given by $\frac{v(x)u'(x) - u(x)v'(x)}{(v(x))^2}$ . Here, $u(x) = x$ and $v(x) = 3 - 4x^3$ .
Differentiate $u(x)$ : Differentiate $u(x)$ with respect to $x$ . The derivative of $u(x) = x$ with respect to $x$ is $u'(x) = 1$ .
Differentiate $v(x)$ : Differentiate $v(x)$ with respect to $x$ . The derivative of $v(x) = 3 - 4x^3$ with respect to $x$ is $v'(x) = -12x^2$ .
Substitute into Formula: Substitute $u(x)$ , $u'(x)$ , $v(x)$ , and $v'(x)$ into the quotient rule formula. $\newline$ Using the quotient rule, we get $f'(x) = \frac{(3 - 4x^3)(1) - (x)(-12x^2)}{(3 - 4x^3)^2}$ .
Simplify Expression: Simplify the expression. $\newline$ Simplify the numerator: $(3 - 4x^3)(1) - (x)(-12x^2) = 3 - 4x^3 + 12x^3$ . $\newline$ Combine like terms: $3 + 8x^3$ . $\newline$ Now, $f'(x) = \frac{3 + 8x^3}{(3 - 4x^3)^2}$ .

More problems from Write a formula for an arithmetic sequence

Question

Find the sum of the finite arithmetic series.

\sum_{n=1}^{10} (7n+4)

\newline

Posted 3 months ago

Question

Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`

Posted 2 months ago

Question

Type the missing number in this sequence: `2, 4 8`, ______,`32`

Posted 2 months ago

Question

What kind of sequence is this?

2, 10, 50, 250, \ldots

Choices:Choices:

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 2 months ago

Question

What is the missing number in this pattern?

1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_

Posted 2 months ago

Question

Classify the series.

\sum_{n = 0}^{12} (n + 2)^3

\newline

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 2 months ago

Question

Find the first three partial sums of the series.

\newline

1 + 6 + 11 + 16 + 21 + 26 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 2 months ago

Question

Find the third partial sum of the series.

\newline

3 + 9 + 15 + 21 + 27 + 33 + \cdots

\newline

Write your answer as an integer or a fraction in simplest form.

\newline

S_3 =

Posted 2 months ago

Question

Find the first three partial sums of the series.

\newline

1 + 7 + 13 + 19 + 25 + 31 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 3 months ago

Question

Does the infinite geometric series converge or diverge?

\newline

1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots

\newline

\newline

\text{[A]converge}

\newline

\text{[B]diverge}

Posted 2 months ago