Full solution
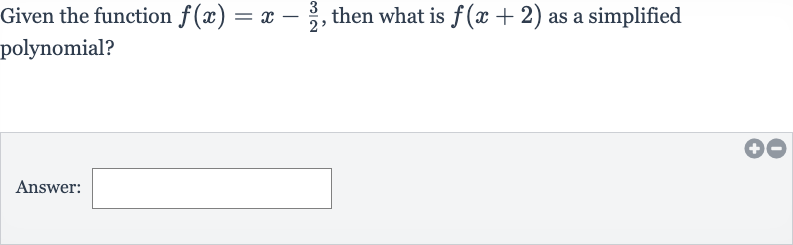
Q. Given the function , then what is as a simplified polynomial?Answer:
- Substitute with : Substitute with in the function . We have the function . To find , we replace every in the function with .
- Simplify the expression: Simplify the expression.Now we simplify the expression by combining like terms.To subtract from , we need a common denominator. The common denominator is , so we convert to .
- Combine like terms: Continue simplifying by combining the fractions.Now we subtract the fractions.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help