Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

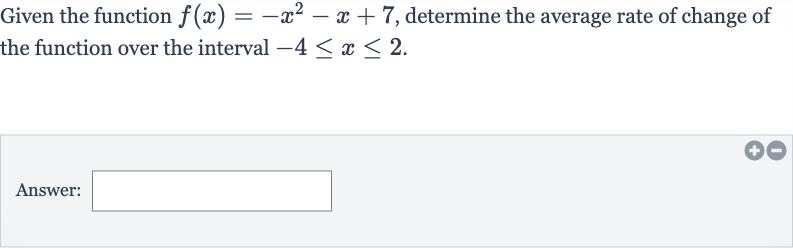
Given the function f(x)=-x^(2)-x+7, determine the average rate of change of the function over the interval -4 <= x <= 2. Answer:

Given the function f(x)=−x2−x+7 f(x)=-x^{2}-x+7 , determine the average rate of change of the function over the interval −4≤x≤2 -4 \leq x \leq 2 .\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Average rate of changeright chevron icon

Full solution

Q. Given the function f(x)=−x2−x+7 f(x)=-x^{2}-x+7 , determine the average rate of change of the function over the interval −4≤x≤2 -4 \leq x \leq 2 .\newlineAnswer:
  1. Identify formula and interval: Identify the average rate of change formula and the given interval.\newlineThe average rate of change of a function f(x)f(x) over an interval [a,b][a, b] is given by the formula:\newlineAverage rate of change = f(b)−f(a)b−a\frac{f(b) - f(a)}{b - a}\newlineFor the given function f(x)=−x2−x+7f(x) = -x^2 - x + 7, we need to find the average rate of change over the interval [−4,2][-4, 2].
  2. Calculate f(−4)f(-4): Calculate the value of f(−4)f(-4).\newlineSubstitute x=−4x = -4 into the function f(x)f(x) to find f(−4)f(-4).\newlinef(−4)=−(−4)2−(−4)+7f(-4) = -(-4)^2 - (-4) + 7\newlinef(−4)=−(16)+4+7f(-4) = -(16) + 4 + 7\newlinef(−4)=−16+4+7f(-4) = -16 + 4 + 7\newlinef(−4)=−12+7f(-4) = -12 + 7\newlinef(−4)=−5f(-4) = -5
  3. Calculate f(2)f(2): Calculate the value of f(2)f(2).\newlineSubstitute x=2x = 2 into the function f(x)f(x) to find f(2)f(2).\newlinef(2)=−(2)2−(2)+7f(2) = -(2)^2 - (2) + 7\newlinef(2)=−4−2+7f(2) = -4 - 2 + 7\newlinef(2)=−6+7f(2) = -6 + 7\newlinef(2)=1f(2) = 1
  4. Use average rate of change formula: Use the average rate of change formula with the values found for f(−4)f(-4) and f(2)f(2).\newlineAverage rate of change = f(2)−f(−4)2−(−4)\frac{f(2) - f(-4)}{2 - (-4)}\newlineAverage rate of change = 1−(−5)2+4\frac{1 - (-5)}{2 + 4}\newlineAverage rate of change = 1+56\frac{1 + 5}{6}\newlineAverage rate of change = 66\frac{6}{6}\newlineAverage rate of change = 11

More problems from Average rate of change

Question
What is the domain of this function?\newline(9,–2)(6,–10)(–3,9)(5,2)(9,–2)(6,–10)(–3,9)(5,2)\newlineChoices:\newline(A){–3,5,6,9}(B){–10,–2,2,9}(C){2,5,6,9}(D){–6,–3,5,9}(A)\{–3,5,6,9\}\newline(B)\{–10,–2,2,9\}\newline(C)\{2,5,6,9\}\newline(D)\{–6,–3,5,9\}
Get tutor helpright-arrow

Posted 1 month ago

Question
Look at this set of ordered pairs:\newline(2,14)(2, 14)\newline(10,12)(10, 12)\newline(3,−19)(3, -19)\newlineIs this relation a function?\newlineChoices:\newline[[yes]\text{[[yes]}[no]]\text{[no]]}
Get tutor helpright-arrow

Posted 1 month ago

Question
Use the following function rule to find f(11) f(11) .\newlinef(x)=−10−7x f(x) = -10 - 7x \newlinef(11)= f(11) = _____
Get tutor helpright-arrow

Posted 1 month ago

Question
Find the slope of the line y=−3x−25 y = -3x - \frac{2}{5} .\newlineSimplify your answer and write it as a proper fraction, improper fraction, or integer.\newline_____\_\_\_\_\_
Get tutor helpright-arrow

Posted 1 month ago

Question
A line has a slope of 33 and passes through the point (−2,−10)(-2,-10). Write its equation in slope-intercept form.\newlineWrite your answer using integers, proper fractions, and improper fractions in simplest form.
Get tutor helpright-arrow

Posted 1 month ago

Question
What is the range of this function?\newliney = |x|\newlineChoices:\newlineall real numbers\text{all real numbers}\newline{y∣y≥0}\{y \mid y \geq 0\}\newline{y∣y≤0}\{y \mid y \leq 0\}\newline{y∣y>0}\{y \mid y > 0\}
Get tutor helpright-arrow

Posted 2 months ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 1 1 unit down of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the domain of this function?\newline(8,–1)(7,–11)(–4,10)(4,3)(8,–1)(7,–11)(–4,10)(4,3)\newlineChoices: \newline(A){–4,4,7,8}(A)\{–4,4,7,8\}\newline(B){–11,–1,3,10}(B)\{–11,–1,3,10\}\newline(C){3,4,7,8}(C)\{3,4,7,8\}\newline(D){–7,–4,4,8}(D)\{–7,–4,4,8\}
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the domain of this function?\newline(10, –3)(2, –9)(–5, 8)(3, 1)(10,\,–3)(2,\,–9)(–5,\,8)(3,\,1)\newlineChoices:\newline[{–5,2,3,10}][{–9, –3,1,8}][{1,2,3,10}][{–10, –5,2,3}][\{–5,2,3,10\}][\{–9,\,–3,1,8\}][\{1,2,3,10\}][\{–10,\,–5,2,3\}]
Get tutor helpright-arrow

Posted 1 month ago

Question
What is the domain of this function?\newline(1,–4)(9,–12)(–6,11)(7,5)(1,–4)(9,–12)(–6,11)(7,5)\newlineChoices:(A){–6,1,7,9}\newline\\(A)\{–6,1,7,9\}\newline(B){–12,–4,5,11}(B)\{–12,–4,5,11\}\newline(C{5,1,7,9}(C\{5,1,7,9\}\newline(D){–9,–6,1,7}(D)\{–9,–6,1,7\}
Get tutor helpright-arrow

Posted 1 month ago

View all (25)