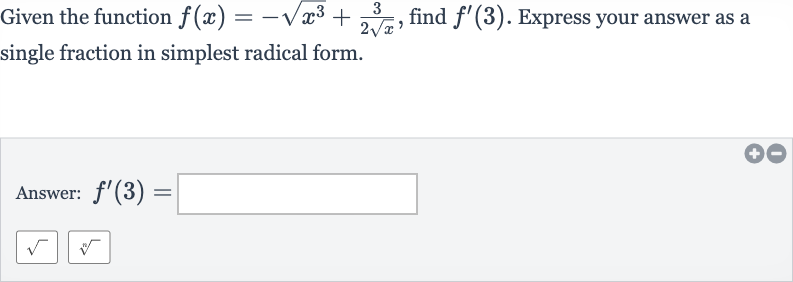
Given the function f(x)=-sqrt(x^(3))+(3)/(2sqrtx), find f^(')(3). Express your answer as a single fraction in simplest radical form. Answer: f^(')(3)=

Question

Given the function  f(x)=-sqrt(x^(3))+(3)/(2sqrtx), find  f^(')(3). Express your answer as a single fraction in simplest radical form. Answer:  f^(')(3)=

Bytelearn · Accepted Answer

Find Derivative of f(x): First, we need to find the derivative of the function f(x) = -√(x^3) + (3)/(2√x). To do this, we will use the power rule and the chain rule for derivatives. f(x) = -x^(3/2) + (3)/(2x^(1/2)) Let's differentiate each term separately.Apply Power Rule: For the first term -x^(3/2), we apply the power rule which states that the derivative of x^n is n*x^(n-1). The derivative of -x^(3/2) is -((3/2)*x^(3/2 - 1)) = -((3/2)*x^(1/2)).Combine Derivatives: For the second term (3)/(2x^(1/2)), we also apply the power rule. The derivative of x^(-1/2) is (-1/2)*x^(-1/2 - 1) = (-1/2)*x^(-3/2). The derivative of (3)/(2x^(1/2)) is (3/2) * (-1/2)*x^(-3/2) = -(3/4)*x^(-3/2).Evaluate at x = 3: Now, we combine the derivatives of both terms to get the derivative of the entire function f(x). f'(x) = -((3/2)*x^(1/2)) - (3/4)*x^(-3/2)Simplify Powers of 3: Next, we need to evaluate the derivative at x = 3. f'(3) = -((3/2)*3^(1/2)) - (3/4)*3^(-3/2)Substitute Values: We simplify the expression by calculating the powers of 3. 3^(1/2) is the square root of 3, which we can write as √3. 3^(-3/2) is 1 over the square root of 3 cubed, which simplifies to 1/(3√3).Perform Multiplication and Division: Now we substitute these values into the derivative. f'(3) = -((3/2)*√3) - (3/4)*(1/(3√3))Find Common Denominator: We simplify the expression by performing the multiplication and division. f'(3) = -(3√3/2) - (1/(4√3))Combine Numerators: To combine these terms into a single fraction, we need a common denominator. The common denominator will be 4√3. f'(3) = -(6√3)/(4√3) - (1)/(4√3)Simplify Numerator: Now we can combine the numerators over the common denominator. f'(3) = (-(6√3) - 1)/(4√3)Finally, we simplify the numerator. f'(3) = (-6√3 - 1)/(4√3) This is the derivative of the function f(x) at x = 3 in simplest radical form.

Given the function $f(x)=-\sqrt{x^{3}}+\frac{3}{2 \sqrt{x}}$ , find $f^{\prime}(3)$ . Express your answer as a single fraction in simplest radical form. $\newline$ Answer: $f^{\prime}(3)=$

Full solution

More problems from Find trigonometric ratios using multiple identities

Related topics

Given the function f(x)=−x3+32x f(x)=-\sqrt{x^{3}}+\frac{3}{2 \sqrt{x}} f(x)=−x3​+2x​3​, find f′(3) f^{\prime}(3) f′(3). Express your answer as a single fraction in simplest radical form.\newlineAnswer: f′(3)= f^{\prime}(3)= f′(3)=

Given the function $f(x)=-\sqrt{x^{3}}+\frac{3}{2 \sqrt{x}}$ , find $f^{\prime}(3)$ . Express your answer as a single fraction in simplest radical form. $\newline$ Answer: $f^{\prime}(3)=$