Full solution
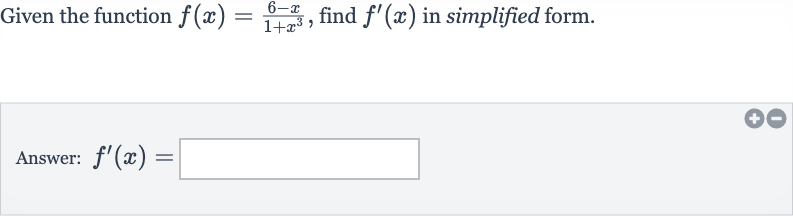
Q. Given the function , find in simplified form.Answer:
- Identify function: Identify the function to differentiate.We have the function . We need to find its derivative, denoted as .
- Apply quotient rule: Apply the quotient rule for differentiation.The quotient rule states that if we have a function , then . Here, and .
- Differentiate and : Differentiate and ., since the derivative of is and the derivative of is ., since the derivative of is and the derivative of is .
- Apply quotient rule: Apply the quotient rule using the derivatives from Step ..
- Expand and simplify: Expand and simplify the numerator of the derivative. .
- Combine like terms: Combine like terms in the numerator..
- Check for simplification: Check for any possible simplification.The numerator and denominator are already in their simplest form, so no further simplification is possible.
More problems from Find the vertex of the transformed function
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help