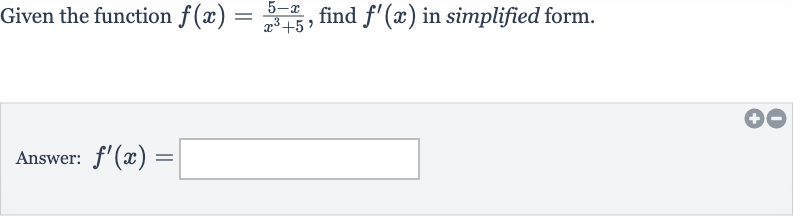
Given the function f(x)=(5-x)/(x^(3)+5), find f^(')(x) in simplified form. Answer: f^(')(x)=

Question

Given the function  f(x)=(5-x)/(x^(3)+5), find  f^(')(x) in simplified form. Answer:  f^(')(x)=

Bytelearn · Accepted Answer

Identify u(x) and v(x): We need to find the derivative of the function f(x) = (5 - x) / (x^3 + 5). To do this, we will use the quotient rule for derivatives, which states that if we have a function in the form of u(x) / v(x), its derivative f'(x) is given by (u'(x)v(x) - u(x)v'(x)) / (v(x))^2.Find Derivatives of u(x) and v(x): First, let's identify u(x) and v(x) from our function f(x). We have u(x) = 5 - x and v(x) = x^3 + 5.Apply Quotient Rule: Now, we need to find the derivatives of u(x) and v(x). The derivative of u(x) with respect to x is u'(x) = -1, since the derivative of a constant is 0 and the derivative of -x is -1. The derivative of v(x) with respect to x is v'(x) = 3x^2, since the derivative of x^3 is 3x^2 and the derivative of a constant is 0.Simplify Numerator: Using the quotient rule, we can now find f'(x) by substituting u(x), u'(x), v(x), and v'(x) into the formula. This gives us f'(x) = ((-1)(x^3 + 5) - (5 - x)(3x^2)) / (x^3 + 5)^2.Combine Like Terms: Next, we simplify the numerator of the derivative. This involves distributing the -1 and -3x^2 across the respective terms and combining like terms. We get f'(x) = (-x^3 - 5 - 15x^2 + 3x^3) / (x^3 + 5)^2.Finalize Derivative: Further simplifying the numerator, we combine the x^3 terms and the constant terms. This gives us f'(x) = (2x^3 - 15x^2 - 5) / (x^3 + 5)^2.The derivative f'(x) is now in simplified form. There are no common factors that can be canceled out between the numerator and the denominator, and the expression is as simplified as it can be.

Given the function $f(x)=\frac{5-x}{x^{3}+5}$ , find $f^{\prime}(x)$ in simplified form. $\newline$ Answer: $f^{\prime}(x)=$

Full solution

More problems from Find the vertex of the transformed function

Related topics

Given the function f(x)=5−xx3+5 f(x)=\frac{5-x}{x^{3}+5} f(x)=x3+55−x​, find f′(x) f^{\prime}(x) f′(x) in simplified form.\newlineAnswer: f′(x)= f^{\prime}(x)= f′(x)=

Given the function $f(x)=\frac{5-x}{x^{3}+5}$ , find $f^{\prime}(x)$ in simplified form. $\newline$ Answer: $f^{\prime}(x)=$