Resources

Testimonials

Plans

Resources

Testimonials

Plans

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

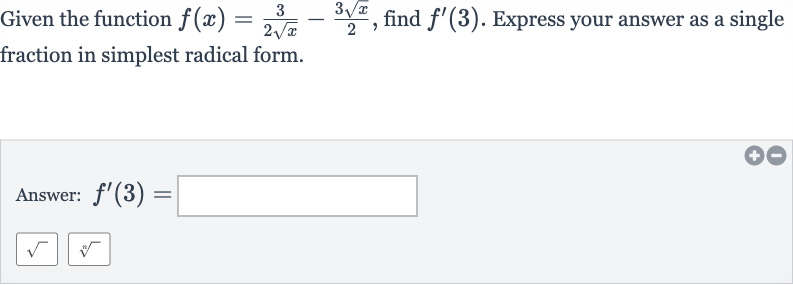
$Given the function f(x)=(3)/(2sqrtx)-(3sqrtx)/(2), find f^(')(3). Express your answer as a single fraction in simplest radical form. Answer: f^(')(3)=$

Given the function $f(x)=\frac{3}{2 \sqrt{x}}-\frac{3 \sqrt{x}}{2}$ , find $f^{\prime}(3)$ . Express your answer as a single fraction in simplest radical form. $\newline$ Answer: $f^{\prime}(3)=$

View step-by-step help

Home

Math Problems

Precalculus

Find trigonometric ratios using multiple identities

Full solution

Q. Given the function

f(x)=\frac{3}{2 \sqrt{x}}-\frac{3 \sqrt{x}}{2}

, find

f^{\prime}(3)

. Express your answer as a single fraction in simplest radical form.

\newline

Answer:

f^{\prime}(3)=

Rewrite function: First, we need to find the derivative of the function $f(x) = \frac{3}{2\sqrt{x}} - \frac{3\sqrt{x}}{2}$ . Let's start by rewriting the function in a form that makes it easier to differentiate. $f(x) = \frac{3}{2x^{\frac{1}{2}}} - \frac{3}{2}x^{\frac{1}{2}}$
Differentiate function: Now, let's differentiate the function using the power rule, which states that the derivative of $x^n$ with respect to $x$ is $n*x^{(n-1)}$ . $\newline$ $f'(x) = \frac{d}{dx}\left[\frac{3}{2x^{(1/2)}}\right] - \frac{d}{dx}\left[\frac{3}{2}x^{(1/2)}\right]$ $\newline$ $f'(x) = \left(\frac{3}{2}\right) * \left(-\frac{1}{2}\right) * x^{(-3/2)} - \left(\frac{3}{2}\right) * \left(\frac{1}{2}\right) * x^{(-1/2)}$
Simplify derivative: Simplify the expression for the derivative. $f'(x) = -(\frac{3}{4})x^{(-\frac{3}{2})} - (\frac{3}{4})x^{(-\frac{1}{2})}$
Evaluate at $x=3$ : Now, we need to evaluate the derivative at $x = 3$ . $f'(3) = -(\frac{3}{4})3^{(-\frac{3}{2})} - (\frac{3}{4})3^{(-\frac{1}{2})}$
Calculate values: Calculate the values of $3^{-\frac{3}{2}}$ and $3^{-\frac{1}{2}}$ . $\newline$ $3^{-\frac{3}{2}} = \frac{1}{3^{\frac{3}{2}}} = \frac{1}{\sqrt{3^3}} = \frac{1}{\sqrt{27}} = \frac{1}{3\sqrt{3}}$ $\newline$ $3^{-\frac{1}{2}} = \frac{1}{3^{\frac{1}{2}}} = \frac{1}{\sqrt{3}}$
Substitute values: Substitute these values into the expression for $f'(3)$ . $f'(3) = -\left(\frac{3}{4}\right)\left(\frac{1}{3\sqrt{3}}\right) - \left(\frac{3}{4}\right)\left(\frac{1}{\sqrt{3}}\right)$
Combine terms: Simplify the expression by combining the terms. $\newline$ $f'(3) = -(\frac{1}{4})(\frac{1}{\sqrt{3}}) - (\frac{3}{4})(\frac{1}{\sqrt{3}})$ $\newline$ $f'(3) = -\frac{1}{4\sqrt{3}} - \frac{3}{4\sqrt{3}}$ $\newline$ $f'(3) = \frac{(-1 - 3)}{4\sqrt{3}}$ $\newline$ $f'(3) = -\frac{4}{4\sqrt{3}}$
Simplify expression: Simplify the fraction by canceling out common factors. $\newline$ $f'(3) = -\frac{1}{\sqrt{3}}$