Full solution
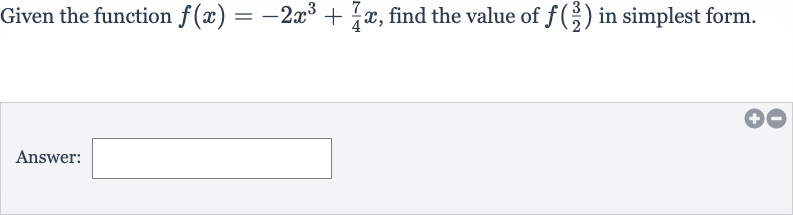
Q. Given the function , find the value of in simplest form.Answer:
- Substitute into function: Substitute the value of into the function.We are given and we need to find . Let's substitute into the function.
- Calculate cube of : Calculate the cube of .
- Multiply by : Multiply the result by -2").\(\newline\$-2 \times \left(\frac{27}{8}\right) = -\frac{54}{8}\)
- Simplify fraction \(-\frac{54}{8}\): Simplify the fraction \(-\frac{54}{8}\).\(-\frac{54}{8}\) can be simplified by dividing both the numerator and the denominator by \(2\).\(-\frac{54}{8} = -\frac{27}{4}\)
- Multiply \((\frac{7}{4})\) by \((\frac{\(3\)}{\(2\)}): Multiply \((\frac{7}{4})\) by \((\frac{3}{2}).\(\newline\)\$(\frac{7}{4}) \times (\frac{3}{2}) = \frac{21}{8}\)
- Add results: Add the two results together.\(\newline\)\(f\left(\frac{3}{2}\right) = -\frac{27}{4} + \frac{21}{8}\)\(\newline\)To add these two fractions, we need a common denominator. The common denominator for \(4\) and \(8\) is \(8\).
- Convert \(-\frac{27}{4}\) to fraction: Convert \(-\frac{27}{4}\) to a fraction with a denominator of \(8\).\(-\frac{27}{4} = -\frac{27}{4} \times \frac{2}{2} = -\frac{54}{8}\)
- Add fractions: Add the fractions with the common denominator.\(\newline\)\(f\left(\frac{3}{2}\right) = -\frac{54}{8} + \frac{21}{8}\)\(\newline\)\(f\left(\frac{3}{2}\right) = \frac{-54 + 21}{8}\)\(\newline\)\(f\left(\frac{3}{2}\right) = -\frac{33}{8}\)
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help