Full solution
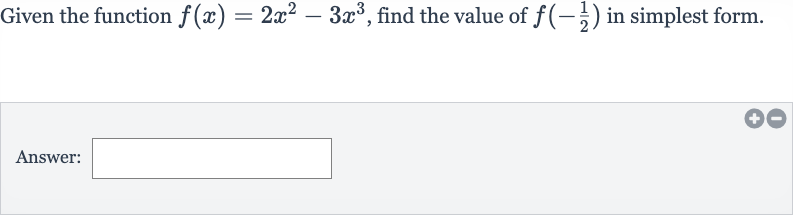
Q. Given the function , find the value of in simplest form.Answer:
- Substitute : Substitute with in the function f\left(-\left(\frac{\(1\)}{\(2\)}\right)\right) = \(2\left(-\frac{}{}\right)^ - \left(-\frac{}{}\right)^
- Calculate square and cube: Calculate the square and cube of . and
- Replace exponents in function: Replace the exponents in the function with their calculated values.
- Multiply coefficients by exponents: Multiply the coefficients by the calculated exponents.
- Simplify expression: Simplify the expression by adding the fractions.To add these fractions, find a common denominator.
- Find common denominator: The common denominator for and is .Convert to a fraction with a denominator of .
- Convert to fraction: Add the fractions with the common denominator.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help