Full solution
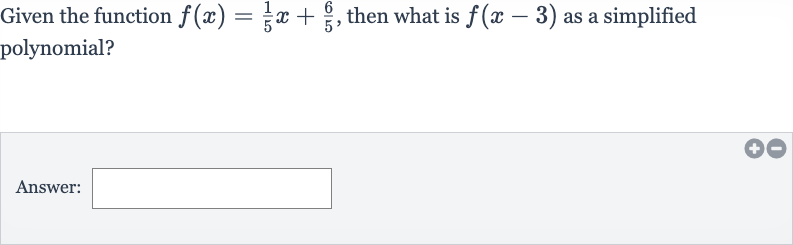
Q. Given the function , then what is as a simplified polynomial?Answer:
- Substitute into function: Substitute into the function . We have the function . To find , we replace every instance of in the function with .
- Distribute across terms: Distribute the across the terms inside the parentheses.We need to multiply by both and .
- Simplify the expression: Simplify the expression.Now we simplify the multiplication and combine any like terms if possible.
- Combine constant terms: Combine the constant terms.We have two constant terms, and , which we can add together.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help