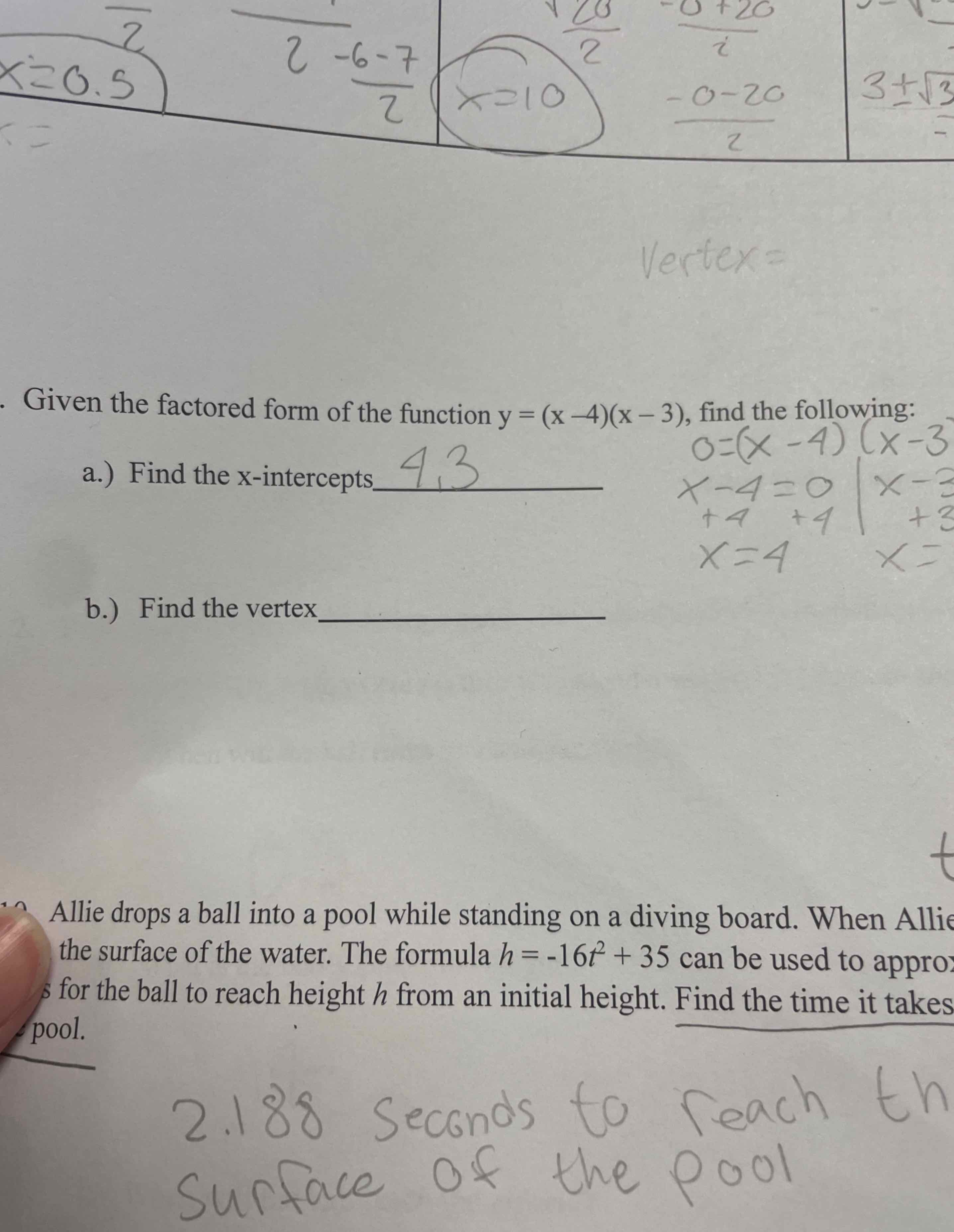Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Given the factored form of the function
y=(x-4)(x-3), find the following:
a.) Find the
x-intercepts
qquad
b.) Find the vertex
qquad

Given the factored form of the function $\newline$ $y=(x-4)(x-3)$ , find the following: $\newline$ a.) Find the $x$ -intercepts $\newline$ b.) Find the vertex

View step-by-step help

View step-by-step help

Solve quadratic equations: word problems

Full solution

Q. Given the factored form of the function

\newline

y=(x-4)(x-3)

, find the following:

\newline

a.) Find the

x

-intercepts

\newline

b.) Find the vertex

Identify x-intercepts: Identify the x-intercepts by setting $y = 0$ and solving for $x$ . $y = (x-4)(x-3) = 0$ $x - 4 = 0$ or $x - 3 = 0$ $x = 4$ or $x = 3$
Calculate vertex: Calculate the vertex using the formula for the vertex of a parabola given in factored form, which is the midpoint of the x-intercepts and the y-value by substituting this x-value back into the equation. $\newline$ Midpoint of $x = 4$ and $x = 3$ is $\frac{4+3}{2} = 3.5$ $\newline$ y = $(3.5-4)(3.5-3) = (-0.5)(0.5) = -0.25$ $\newline$ Vertex = $(3.5, -0.25)$

More problems from Solve quadratic equations: word problems

Question

Solve by completing the square.

\newline

m^2 - 10m - 29 = 0

\newline

Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.

\newline

`m` = ____ or `m` = _____

Posted 8 months ago

Question

g(x)

g(x)

is the translation

5

f(x)=x^2

\newline

Write your answer in the form

a(x–h)^2+k

a

h

k

\newline

g(x)=

Posted 7 months ago

Question

What is the range of this quadratic function?

\newline

y = x^2 - 4x + 4

\newline

\newline

\left\{y \mid y \geq 2\right\}

\newline

\left\{y \mid y \leq 0\right\}

\newline

\left\{y \mid y \geq 0\right\}

\newline

\text{all real numbers}

Posted 5 months ago

Question

Write the equation of the parabola that passes through the points

(1,0)

(2,0)

(3,\text{–}16)

. Write your answer in the form

y = a(x – p)(x – q)

a

p

q

are integers, decimals, or simplified fractions.

\newline

Posted 5 months ago

Question

Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.

\newline

f^2 + 8f + \_\_\_\_\_

Posted 5 months ago

Question

h

\newline

h^2 + 39h = 0

\newline

\newline

Write each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.

\newline

h =

\newline

Posted 5 months ago

Question

Write a quadratic function with zeros

-9

-7

\newline

Write your answer using the variable

x

and in standard form with a leading coefficient of

1

\newline

f(x) = \_\_\_\_\_

Posted 5 months ago

Question

Find the equation of the axis of symmetry for the parabola

y = x^2

\newline

Simplify any numbers and write them as proper fractions, improper fractions, or integers.

\newline

\underline{\hspace{3cm}}

Posted 4 months ago

Question

g(x)

g(x)

is the translation

8

f(x) = x^2

\newline

Write your answer in the form

a(x – h)^2 + k

a

h

k

\newline

g(x) =

\newline

Posted 4 months ago

Question

x

\newline

x^2 = 1

\newline

\newline

Write your answer in simplified, rationalized form.

\newline

x =

x =

\newline

Posted 5 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant