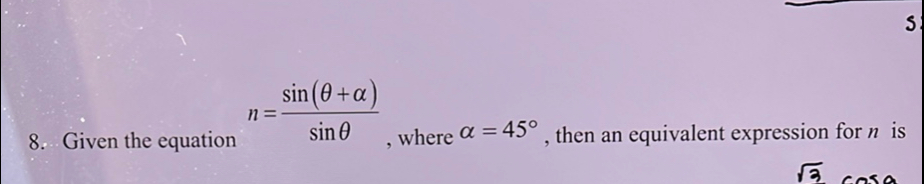Given the equation $n=\frac{\sin (\theta+\alpha)}{\sin \theta}$ , where $\alpha=45^{\circ}$ , then an equivalent expression for $n$ is

View step-by-step help

Home

Math Problems

Algebra 2

Find the vertex of the transformed function

Full solution

Q. Given the equation

n=\frac{\sin (\theta+\alpha)}{\sin \theta}

, where

\alpha=45^{\circ}

, then an equivalent expression for

n

Expand using angle addition formula: Use the angle addition formula for sine to expand $\sin(\theta + \alpha)$ . The angle addition formula for sine is $\sin(A + B) = \sin(A)\cos(B) + \cos(A)\sin(B)$ . Here, $A = \theta$ and $B = \alpha = 45$ degrees. $\sin(\theta + 45$ degrees) = $\sin(\theta)\cos(45$ degrees) + $\cos(\theta)\sin(45$ degrees).
Substitute values and simplify: Substitute the values of $\sin(45^\circ)$ and $\cos(45^\circ)$ . Since $\sin(45^\circ) = \cos(45^\circ) = \sqrt{2}/2$ , we can substitute these values into the expanded expression. $\sin(\theta + 45^\circ) = \sin(\theta)(\sqrt{2}/2) + \cos(\theta)(\sqrt{2}/2)$ .
Substitute into equation for $n$ : Substitute the expanded expression of $\sin(\theta + 45^\circ)$ into the equation for $n$ .
$n = \frac{\sin(\theta + 45^\circ)}{\sin \theta}$
$n = \frac{\sin(\theta)\left(\frac{\sqrt{2}}{2}\right) + \cos(\theta)\left(\frac{\sqrt{2}}{2}\right)}{\sin \theta}$ .
Simplify numerator terms: Simplify the expression by dividing each term in the numerator by $\sin(\theta)$ . $\newline$ $n = \left(\frac{\sin(\theta)\left(\frac{\sqrt{2}}{2}\right)}{\sin(\theta)}\right) + \left(\frac{\cos(\theta)\left(\frac{\sqrt{2}}{2}\right)}{\sin(\theta)}\right)$ $\newline$ $n = \left(\frac{\sqrt{2}}{2}\right) + \left(\frac{\cos(\theta)}{\sin(\theta)}\right)\left(\frac{\sqrt{2}}{2}\right)$ .
Use cotangent identity: Recognize that $\cos(\theta)/\sin(\theta)$ is the cotangent of $\theta$ . $\newline$ $\cot(\theta) = \cos(\theta)/\sin(\theta)$ . $\newline$ Substitute $\cot(\theta)$ into the expression. $\newline$ $n = (\sqrt{2}/2) + \cot(\theta)(\sqrt{2}/2)$ .
Factor out common factor: Factor out the common factor of $\frac{\sqrt{2}}{2}$ . $\newline$ $n = \left(\frac{\sqrt{2}}{2}\right)(1 + \cot(\theta))$ .