Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

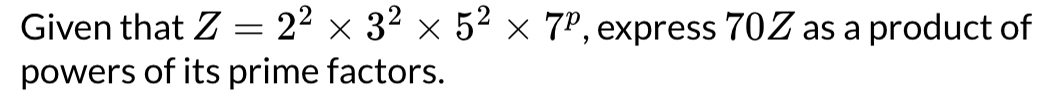
Given that Z=2^(2)×3^(2)×5^(2)×7^(p), express 70 Z as a product of powers of its prime factors.

Given that $Z=2^{2} \times 3^{2} \times 5^{2} \times 7^{p}$ , express $70 Z$ as a product of powers of its prime factors.

View step-by-step help

View step-by-step help

Prime factorization with exponents

Full solution

Q. Given that

Z=2^{2} \times 3^{2} \times 5^{2} \times 7^{p}

, express

70 Z

as a product of powers of its prime factors.

Identify Prime Factors: Identify the prime factors of $70$ . The prime factors of $70$ are $2$ , $5$ , and $7$ .
Express as Product: Express $70$ as a product of powers of its prime factors. Since $70 = 2 \times 5 \times 7$ , we can write it as $2^{1}\times5^{1}\times7^{1}$ .
Combine with Z: Combine the prime factorization of $70$ with $Z$ . We have $Z = 2^{2}\times3^{2}\times5^{2}\times7^{p}$ and $70 = 2^{1}\times5^{1}\times7^{1}$ . Multiplying these together, we get $70Z = (2^{2}\times3^{2}\times5^{2}\times7^{p}) \times (2^{1}\times5^{1}\times7^{1})$ .
Combine Like Terms: Use the property of exponents that states $a^{m} \times a^{n} = a^{m+n}$ to combine like terms. For the prime factor $2$ , we have $2^{2} \times 2^{1} = 2^{2+1} = 2^{3}$ . For the prime factor $5$ , we have $5^{2} \times 5^{1} = 5^{2+1} = 5^{3}$ . For the prime factor $7$ , we have $7^{p} \times 7^{1} = 7^{p+1}$ . The prime factor $3$ remains unchanged as it is not a factor of $70$ .
Final Expression: Write the final expression for $70Z$ as a product of powers of its prime factors. The final expression is $70Z = 2^{3}\times3^{2}\times5^{3}\times7^{p+1}.$

More problems from Prime factorization with exponents

Question

The Huffman Corporation would like to donate

15

20

printers to local schools. The corporation would like to make sure that each school receives the same set of computers and printers, with none left over. What is the greatest number of schools that The Huffman Corporation can donate to?

\newline

\_\_\_\_

Posted 3 months ago

Question

What is the greatest common factor of

2

14

\newline

Posted 3 months ago

Question

What is the least common multiple of

6

12

\newline

Posted 3 months ago

Question

Which numbers are factors of

20

? Select all that apply.

\newline

17

\newline

5

\newline

9

\newline

7

Posted 1 month ago

Question

Kris is wrapping Christmas lights around the railing that runs around three sides of his square porch If one side of his porch is

12

feet long, and each strand of his Christmas lights will wrap around a

70

-inch length of the railing, what is the minimum number of strands Kris needs to completely wrap the porch railing?

\newline

6

\newline

7

\newline

8

\newline

9

Posted 2 months ago

Question

What is the greatest common factor of

35 y^{4}, 14 y^{4}

63 y^{4}

Posted 4 months ago

Question

What is the greatest common factor of

60 \mathrm{w}, 36 w^{2}

24 w^{4}

Posted 2 months ago

Question

Find the greatest common factor of

75

8

21

Posted 4 months ago

Question

Find the greatest common factor of

110

40

120

Posted 4 months ago

Question

What is the greatest common factor of

6 a, 8 a^{2}

14

Posted 4 months ago