Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Given that f(x)=x+1,g(x)=-3x and h(x)=-f(x)+3g(x+3), then what is the value of h(3) ? Answer:

Given that f(x)=x+1,g(x)=−3x f(x)=x+1, g(x)=-3 x and h(x)=−f(x)+3g(x+3) h(x)=-f(x)+3 g(x+3) , then what is the value of h(3) h(3) ?\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Find trigonometric ratios using multiple identitiesright chevron icon

Full solution

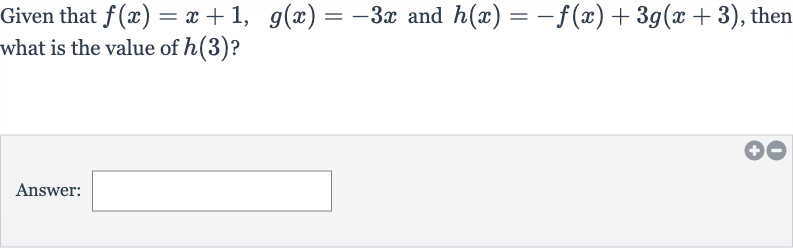
Q. Given that f(x)=x+1,g(x)=−3x f(x)=x+1, g(x)=-3 x and h(x)=−f(x)+3g(x+3) h(x)=-f(x)+3 g(x+3) , then what is the value of h(3) h(3) ?\newlineAnswer:
  1. Find f(3)f(3): First, we need to find the value of f(3)f(3) since it is part of the definition of h(x)h(x).\newlinef(x)=x+1f(x) = x + 1, so f(3)=3+1f(3) = 3 + 1.\newlinef(3)=4f(3) = 4.
  2. Find g(x+3)g(x+3): Next, we need to find the value of g(x+3)g(x+3). Since g(x)=−3xg(x) = -3x, we substitute xx with (x+3)(x+3) to get g(x+3)g(x+3).\newlineg(x+3)=−3(x+3)=−3x−9.g(x+3) = -3(x+3) = -3x - 9.\newlineNow we need to find the value of g(3+3)g(3+3) which is g(6)g(6).\newlineg(6)=−3(6)−9.g(6) = -3(6) - 9.\newlineg(x+3)g(x+3)00\newlineg(x+3)g(x+3)11
  3. Find h(3)h(3): Now we have the values for f(3)f(3) and g(6)g(6), we can find h(3)h(3) using the definition h(x)=−f(x)+3g(x+3)h(x) = -f(x) + 3g(x+3).
    h(3)=−f(3)+3g(6)h(3) = -f(3) + 3g(6).
    h(3)=−(4)+3(−27)h(3) = -(4) + 3(-27).
    h(3)=−4−81h(3) = -4 - 81.
    h(3)=−85h(3) = -85.

More problems from Find trigonometric ratios using multiple identities

Question
If cos⁡(θ)=817 \cos(\theta)=\frac{8}{17} and 0∘<θ<90∘ 0^\circ<\theta<90^\circ , what is sec⁡(θ) \sec(\theta) ? Write your answer in simplified, rationalized form. sec⁡(θ)= \sec(\theta)= ______
Get tutor helpright-arrow

Posted 5 months ago

Question
cos⁡(x)=−0.3\cos(x) = -0.3. What is sin⁡(90∘−x)\sin(90^\circ - x)? ____
Get tutor helpright-arrow

Posted 9 months ago

Question
If csc⁡(θ)=178 \csc(\theta) = \frac{17}{8} and 0∘<θ<90∘ 0^\circ < \theta < 90^\circ , what is tan⁡(θ) \tan(\theta) ?\newlineWrite your answer in simplified, rationalized form.\newlinetan⁡(θ)= \tan(\theta) = ______\newline
Get tutor helpright-arrow

Posted 9 months ago

Question
Is the sine function even or odd?\newlineChoices:\newline[A]even\text{[A]even}\newline[B]odd\text{[B]odd}
Get tutor helpright-arrow

Posted 9 months ago

Question
Write the sentence as an equation. \newline8989 is equal to the quotient of yy and 1717 \newlineType a slash ( / / ) if you want to use a division sign. \newline_____
Get tutor helpright-arrow

Posted 7 months ago

Question
Write the sentence as an equation. \newline4545 is equal to the quotient of zz and 55 \newlineType a slash ( / / ) if you want to use a division sign. \newline_____
Get tutor helpright-arrow

Posted 9 months ago

Question
Solve for hh. \newline h2+24h=0h^2 + 24h = 0 \newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas. \newline h=h = _____
Get tutor helpright-arrow

Posted 10 months ago

Question
h2−4h=0h^2 - 4h = 0
Get tutor helpright-arrow

Posted 7 months ago

Question
Combine the like terms to create an equivalent expression:\newline−k−(−8k)=□-k-(-8k)=\square
Get tutor helpright-arrow

Posted 10 months ago

Question
Which of the following degree measures is equal to 5π 5 \pi radians?\newline(The number of degrees of arc in a circle is 360360 . The number of radians of arc in a circle is 2π 2 \pi .)\newlineChoose 11 answer:\newline(A) 144∘ 144^{\circ} \newline(B) 900∘ 900^{\circ} \newline(C) 1,080∘ 1,080^{\circ} \newline(D) 1,800∘ 1,800^{\circ}
Get tutor helpright-arrow

Posted 7 months ago

View all (68)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant