Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Given that f(x)=2x,g(x)=x-2 and h(x)=-3f(x+3)-g(x), then what is the value of h(1) ? Answer:

Given that f(x)=2x,g(x)=x−2 f(x)=2 x, g(x)=x-2 and h(x)=−3f(x+3)−g(x) h(x)=-3 f(x+3)-g(x) , then what is the value of h(1) h(1) ?\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Find trigonometric ratios using multiple identitiesright chevron icon

Full solution

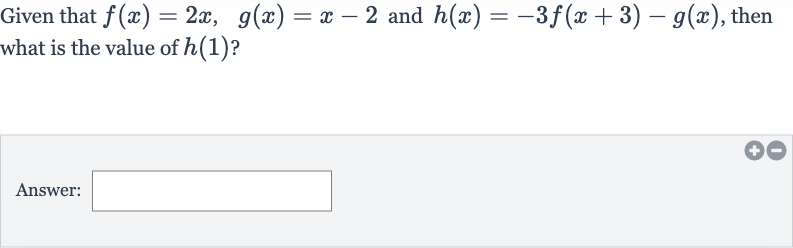
Q. Given that f(x)=2x,g(x)=x−2 f(x)=2 x, g(x)=x-2 and h(x)=−3f(x+3)−g(x) h(x)=-3 f(x+3)-g(x) , then what is the value of h(1) h(1) ?\newlineAnswer:
  1. Write Functions Given: First, let's write down the functions given:\newlinef(x)=2xf(x) = 2x\newlineg(x)=x−2g(x) = x - 2\newlineh(x)=−3f(x+3)−g(x)h(x) = -3f(x + 3) - g(x)\newlineWe need to find the value of h(1)h(1).
  2. Find f(4)f(4): Now, let's find the value of f(x+3)f(x + 3) when x=1x = 1.\newlinef(1+3)=f(4)=2×4=8f(1 + 3) = f(4) = 2 \times 4 = 8
  3. Calculate g(1)g(1): Next, we calculate the value of g(x)g(x) when x=1x = 1.\newlineg(1)=1−2=−1g(1) = 1 - 2 = -1
  4. Substitute Values into h(x)h(x): Now we can substitute the values of f(4)f(4) and g(1)g(1) into the equation for h(x)h(x) to find h(1)h(1).
    h(1)=−3f(1+3)−g(1)h(1) = -3f(1 + 3) - g(1)
    h(1)=−3×8−(−1)h(1) = -3 \times 8 - (-1)
    h(1)=−24+1h(1) = -24 + 1
  5. Simplify to Find h(1)h(1): Finally, we simplify the expression to find the value of h(1)h(1).\newlineh(1)=−24+1=−23h(1) = -24 + 1 = -23

More problems from Find trigonometric ratios using multiple identities

Question
If cos⁡(θ)=817 \cos(\theta)=\frac{8}{17} and 0∘<θ<90∘ 0^\circ<\theta<90^\circ , what is sec⁡(θ) \sec(\theta) ? Write your answer in simplified, rationalized form. sec⁡(θ)= \sec(\theta)= ______
Get tutor helpright-arrow

Posted 2 months ago

Question
cos⁡(x)=−0.3\cos(x) = -0.3. What is sin⁡(90∘−x)\sin(90^\circ - x)? ____
Get tutor helpright-arrow

Posted 2 months ago

Question
If csc⁡(θ)=178 \csc(\theta) = \frac{17}{8} and 0∘<θ<90∘ 0^\circ < \theta < 90^\circ , what is tan⁡(θ) \tan(\theta) ?\newlineWrite your answer in simplified, rationalized form.\newlinetan⁡(θ)= \tan(\theta) = ______\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Is the sine function even or odd?\newlineChoices:\newline[A]even\text{[A]even}\newline[B]odd\text{[B]odd}
Get tutor helpright-arrow

Posted 2 months ago

Question
Write the sentence as an equation. \newline8989 is equal to the quotient of yy and 1717 \newlineType a slash ( / / ) if you want to use a division sign. \newline_____
Get tutor helpright-arrow

Posted 1 month ago

Question
Write the sentence as an equation. \newline4545 is equal to the quotient of zz and 55 \newlineType a slash ( / / ) if you want to use a division sign. \newline_____
Get tutor helpright-arrow

Posted 3 months ago

Question
Solve for hh. \newline h2+24h=0h^2 + 24h = 0 \newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas. \newline h=h = _____
Get tutor helpright-arrow

Posted 3 months ago

Question
h2−4h=0h^2 - 4h = 0
Get tutor helpright-arrow

Posted 1 month ago

Question
Combine the like terms to create an equivalent expression:\newline−k−(−8k)=□-k-(-8k)=\square
Get tutor helpright-arrow

Posted 4 months ago

Question
Which of the following degree measures is equal to 5π 5 \pi radians?\newline(The number of degrees of arc in a circle is 360360 . The number of radians of arc in a circle is 2π 2 \pi .)\newlineChoose 11 answer:\newline(A) 144∘ 144^{\circ} \newline(B) 900∘ 900^{\circ} \newline(C) 1,080∘ 1,080^{\circ} \newline(D) 1,800∘ 1,800^{\circ}
Get tutor helpright-arrow

Posted 1 month ago

View all (71)