Resources

Testimonials

Plans

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

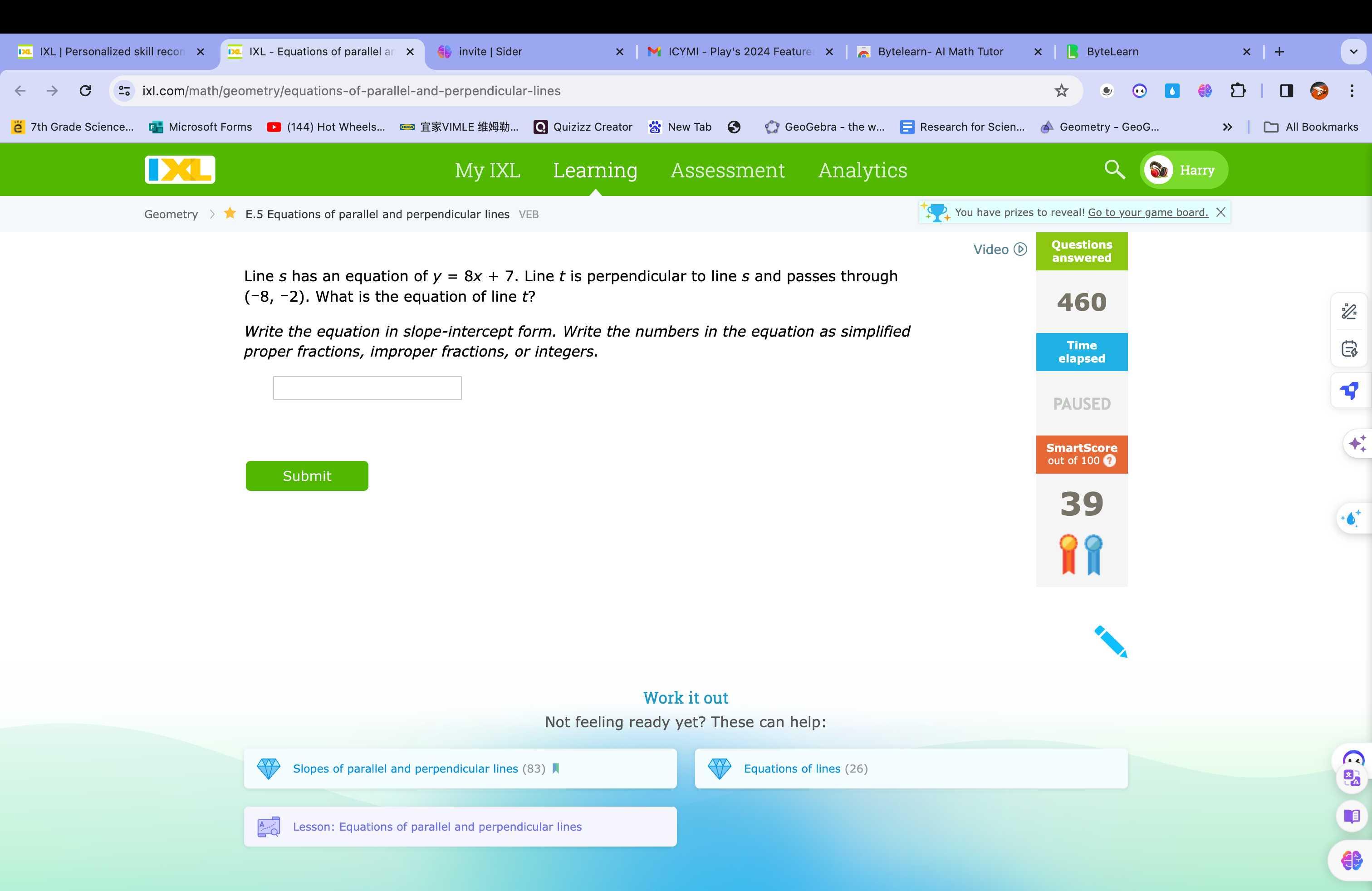
$Line s has an equation of y=8x+7. Line t is perpendicular to line s and passes through (-8,-2). What is the equation of line t ? Write the equation in slope-intercept form. Write the numbers in the equation as simplified proper fractions, improper fractions, or integers.$

Line $s$ has an equation of $y=8 x+7$ . Line $t$ is perpendicular to line $s$ and passes through $(-8,-2)$ . What is the equation of line $t$ ? $\newline$ Write the equation in slope-intercept form. Write the numbers in the equation as simplified proper fractions, improper fractions, or integers.

View step-by-step help

Home

Math Problems

Algebra 2

Solve trigonometric equations I

Full solution

Q. Line

s

has an equation of

y=8 x+7

. Line

t

is perpendicular to line

s

and passes through

(-8,-2)

. What is the equation of line

t

\newline

Write the equation in slope-intercept form. Write the numbers in the equation as simplified proper fractions, improper fractions, or integers.

Find slope of line $s$ : Find the slope of line $s$ . The slope of line $s$ is the coefficient of $x$ in the equation $y = 8x + 7$ , which is $8$ .
Determine slope of line $t$ : Determine the slope of line $t$ . $\newline$ Since line $t$ is perpendicular to line $s$ , its slope will be the negative reciprocal of the slope of line $s$ . The negative reciprocal of $8$ is $-\frac{1}{8}$ .
Use point-slope form: Use the point-slope form to write the equation of line $t$ . The point-slope form of a line is $y - y_1 = m(x - x_1)$ , where $m$ is the slope and $(x_1, y_1)$ is a point on the line. We have $m = -\frac{1}{8}$ and the point $(-8, -2)$ .
Plug slope and point: Plug the slope and point into the point-slope form. $\newline$ $y - (-2) = -\frac{1}{8}(x - (-8))$ $\newline$ $y + 2 = -\frac{1}{8}(x + 8)$
Distribute slope: Distribute the slope on the right side of the equation. $\newline$ $y + 2 = -\frac{1}{8} \times x - \frac{1}{8} \times 8$ $\newline$ $y + 2 = -\frac{1}{8} \times x - 1$
Isolate y: Isolate y to get the slope-intercept form of the equation. $\newline$ $y = -\frac{1}{8} \times x - 1 - 2$ $\newline$ $y = -\frac{1}{8} \times x - 3$