Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

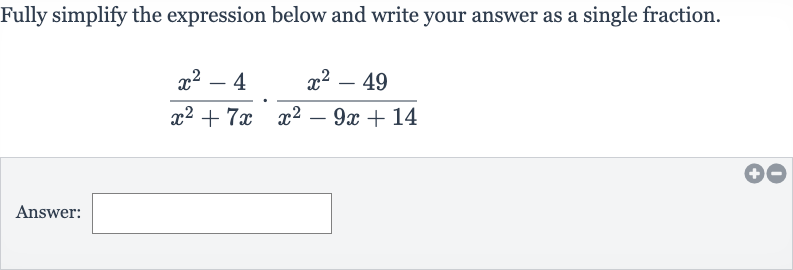
Fully simplify the expression below and write your answer as a single fraction. (x^(2)-4)/(x^(2)+7x)*(x^(2)-49)/(x^(2)-9x+14) Answer:

Fully simplify the expression below and write your answer as a single fraction.\newlinex2−4x2+7x⋅x2−49x2−9x+14 \frac{x^{2}-4}{x^{2}+7 x} \cdot \frac{x^{2}-49}{x^{2}-9 x+14} \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Multiplication with rational exponentsright chevron icon

Full solution

Q. Fully simplify the expression below and write your answer as a single fraction.\newlinex2−4x2+7x⋅x2−49x2−9x+14 \frac{x^{2}-4}{x^{2}+7 x} \cdot \frac{x^{2}-49}{x^{2}-9 x+14} \newlineAnswer:
  1. Factorize Numerators and Denominators: Factor the numerators and denominators where possible.\newlineThe numerator of the first fraction, x2−4x^2 - 4, is a difference of squares and can be factored as (x−2)(x+2)(x - 2)(x + 2).\newlineThe denominator of the second fraction, x2−9x+14x^2 - 9x + 14, can be factored as (x−7)(x−2)(x - 7)(x - 2) because it is a quadratic expression that factors neatly.\newlineThe numerator of the second fraction, x2−49x^2 - 49, is also a difference of squares and can be factored as (x−7)(x+7)(x - 7)(x + 7).
  2. Rewrite with Factored Terms: Rewrite the expression with the factored terms.\newlineThe expression becomes:\newline(x−2)(x+2)x2+7x×(x−7)(x+7)(x−7)(x−2)\frac{(x - 2)(x + 2)}{x^2 + 7x} \times \frac{(x - 7)(x + 7)}{(x - 7)(x - 2)}
  3. Cancel Common Factors: Cancel out the common factors.\newlineThe (x−7)(x - 7) and (x−2)(x - 2) terms are present in both a numerator and a denominator, so they cancel each other out.\newlineThe expression now simplifies to:\newlinex+2x2+7x×(x+7)\frac{x + 2}{x^2 + 7x} \times (x + 7)
  4. Multiply Remaining Terms: Multiply the remaining terms.\newlineNow we multiply the numerators and the denominators:\newlineNumerator: (x+2)×(x+7)(x + 2) \times (x + 7)\newlineDenominator: x2+7xx^2 + 7x
  5. Expand Numerator: Expand the numerator.\newline(x+2)×(x+7)=x2+7x+2x+14=x2+9x+14(x + 2) \times (x + 7) = x^2 + 7x + 2x + 14 = x^2 + 9x + 14
  6. Write Final Expression: Write the final simplified expression.\newlineThe final expression is:\newline(x2+9x+14)/(x2+7x)(x^2 + 9x + 14)/(x^2 + 7x)

More problems from Multiplication with rational exponents

Question
Simplify.\newline811281^{\frac{1}{2}}\newline_____________
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify.\newline(−32)1/5(-32)^{1/5}\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify. Assume all variables are positive.\newlinew43w73\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. Assume all variables are positive.\newline(2r13)8(2r^{\frac{1}{3}})^8\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. Assume all variables are positive.\newlinev74⋅v94v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify.\newline114⋅1141^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. \newline32(−1/5)32^{(-1/5)}
Get tutor helpright-arrow

Posted 7 months ago

Question
Simplify. Assume all variables are positive.\newlinew32w52\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify. Assume all variables are positive.\newline(27x)23(27x)^{\frac{2}{3}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 8 months ago

Question
Simplify. Assume all variables are positive.\newlinex14x114\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 7 months ago

View all (744)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant