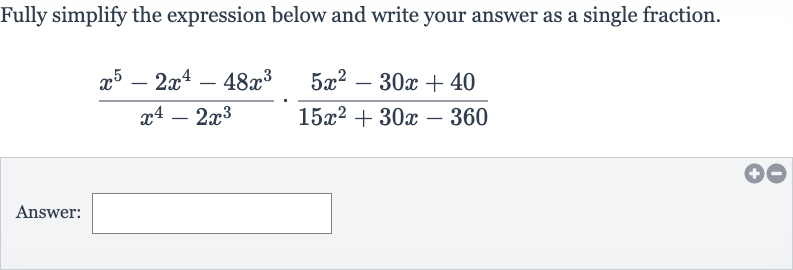
Fully simplify the expression below and write your answer as a single fraction. (x^(5)-2x^(4)-48x^(3))/(x^(4)-2x^(3))*(5x^(2)-30 x+40)/(15x^(2)+30 x-360) Answer:

Question

Fully simplify the expression below and write your answer as a single fraction.  (x^(5)-2x^(4)-48x^(3))/(x^(4)-2x^(3))*(5x^(2)-30 x+40)/(15x^(2)+30 x-360) Answer:

Bytelearn · Accepted Answer

Factorize fractions: Factor the numerator and denominator of the first fraction. We have the first fraction as (x^5 - 2x^4 - 48x^3) / (x^4 - 2x^3). We can factor out an x^3 from both the numerator and the denominator. (x^5 - 2x^4 - 48x^3) / (x^4 - 2x^3) = x^3(x^2 - 2x - 48) / x^3(x - 2)Factorize quadratic expressions: Factor the quadratic expression in the numerator. The quadratic expression x^2 - 2x - 48 can be factored into (x - 8)(x + 6). x^3(x^2 - 2x - 48) / x^3(x - 2) = x^3(x - 8)(x + 6) / x^3(x - 2)Cancel common terms: Cancel out the common x^3 term. The x^3 term in the numerator and denominator cancels out. x^3(x - 8)(x + 6) / x^3(x - 2) = (x - 8)(x + 6) / (x - 2)Factorize second fraction: Factor the numerator and denominator of the second fraction. We have the second fraction as (5x^2 - 30x + 40) / (15x^2 + 30x - 360). We can factor out a 5 from the numerator and a 15 from the denominator. (5x^2 - 30x + 40) / (15x^2 + 30x - 360) = 5(x^2 - 6x + 8) / 15(x^2 + 2x - 24)Cancel common factors: Factor the quadratic expressions in the numerator and denominator. The quadratic expression x^2 - 6x + 8 can be factored into (x - 4)(x - 2), and x^2 + 2x - 24 can be factored into (x + 6)(x - 4). 5(x^2 - 6x + 8) / 15(x^2 + 2x - 24) = 5(x - 4)(x - 2) / 15(x + 6)(x - 4)Multiply fractions: Cancel out the common factors and simplify the constants. The (x - 4) term in the numerator and denominator cancels out, and we can simplify the constants 5/15 to 1/3. 5(x - 4)(x - 2) / 15(x + 6)(x - 4) = (1/3)(x - 2) / (x + 6)Cancel common terms: Multiply the simplified first fraction by the simplified second fraction. Now we multiply (x - 8)(x + 6) / (x - 2) by (1/3)(x - 2) / (x + 6). ((x - 8)(x + 6) / (x - 2)) * ((1/3)(x - 2) / (x + 6)) = (x - 8)(x + 6)(1/3)(x - 2) / ((x - 2)(x + 6))Write final expression: Cancel out the common (x - 2) and (x + 6) terms. The (x - 2) and (x + 6) terms in the numerator and denominator cancel out. (x - 8)(x + 6)(1/3)(x - 2) / ((x - 2)(x + 6)) = (1/3)(x - 8)Write the final simplified expression. The final simplified expression is (1/3)(x - 8), which is the same as (x - 8) / 3.

Fully simplify the expression below and write your answer as a single fraction. $\newline$ $\frac{x^{5}-2 x^{4}-48 x^{3}}{x^{4}-2 x^{3}} \cdot \frac{5 x^{2}-30 x+40}{15 x^{2}+30 x-360}$ $\newline$ Answer:

Full solution

More problems from Multiplication with rational exponents

Related topics