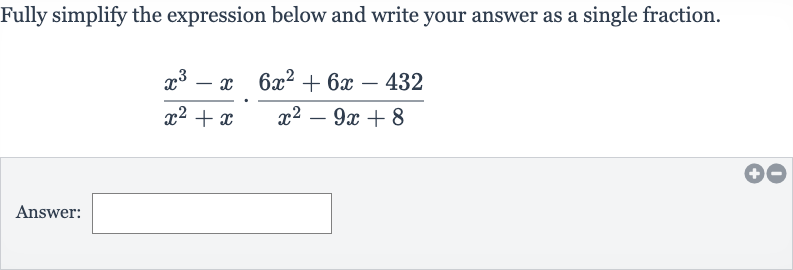
Fully simplify the expression below and write your answer as a single fraction. (x^(3)-x)/(x^(2)+x)*(6x^(2)+6x-432)/(x^(2)-9x+8) Answer:

Question

Fully simplify the expression below and write your answer as a single fraction.  (x^(3)-x)/(x^(2)+x)*(6x^(2)+6x-432)/(x^(2)-9x+8) Answer:

Bytelearn · Accepted Answer

Factor Numerator and Denominator: Factor the numerator and denominator of both fractions where possible. The first fraction's numerator can be factored by recognizing it as a difference of squares: x^3 - x = x(x^2 - 1) = x(x + 1)(x - 1) The first fraction's denominator is already factored: x^2 + x = x(x + 1) The second fraction's numerator does not factor nicely, but we can factor out a common factor of 6: 6x^2 + 6x - 432 = 6(x^2 + x - 72) The second fraction's denominator can be factored as a quadratic: x^2 - 9x + 8 = (x - 1)(x - 8)Rewrite with Factored Terms: Rewrite the expression with the factored terms. Now we have: (x(x + 1)(x - 1) / x(x + 1)) * (6(x^2 + x - 72) / ((x - 1)(x - 8)))Cancel Common Factors: Cancel out the common factors in the numerator and denominator. In the first fraction, x and (x + 1) are common to both the numerator and the denominator, so they cancel out. In the second fraction, (x - 1) is common to both the numerator and the denominator, so it cancels out as well. After canceling, we have: (x - 1) * (6(x^2 + x - 72) / (x - 8))Expand Remaining Terms: Expand the remaining terms in the numerator of the second fraction. We need to distribute the 6 to each term inside the parentheses: 6(x^2 + x - 72) = 6x^2 + 6x - 432 Now the expression looks like this: (x - 1) * ((6x^2 + 6x - 432) / (x - 8))Multiply Remaining Terms: Multiply the remaining terms in the numerator. We multiply (x - 1) by each term in the numerator of the second fraction: (x - 1)(6x^2 + 6x - 432) = 6x^3 + 6x^2 - 6x - 6x^2 - 6x + 432Combine Like Terms: Combine like terms in the numerator. After distributing, we combine the like terms: 6x^3 + 6x^2 - 6x - 6x^2 - 6x + 432 = 6x^3 - 12x + 432 Now the expression is: (6x^3 - 12x + 432) / (x - 8)Check for Further Simplification: Check for any further simplification. We can factor out a 6 from the numerator to see if there is any further simplification: 6x^3 - 12x + 432 = 6(x^3 - 2x + 72) However, the expression x^3 - 2x + 72 does not factor nicely, and there are no common factors with the denominator (x - 8). So, this is the final simplified form.

Fully simplify the expression below and write your answer as a single fraction. $\newline$ $\frac{x^{3}-x}{x^{2}+x} \cdot \frac{6 x^{2}+6 x-432}{x^{2}-9 x+8}$ $\newline$ Answer:

Full solution

More problems from Multiplication with rational exponents

Related topics

Fully simplify the expression below and write your answer as a single fraction.\newlinex3−xx2+x⋅6x2+6x−432x2−9x+8 \frac{x^{3}-x}{x^{2}+x} \cdot \frac{6 x^{2}+6 x-432}{x^{2}-9 x+8} x2+xx3−x​⋅x2−9x+86x2+6x−432​\newlineAnswer:

Fully simplify the expression below and write your answer as a single fraction. $\newline$ $\frac{x^{3}-x}{x^{2}+x} \cdot \frac{6 x^{2}+6 x-432}{x^{2}-9 x+8}$ $\newline$ Answer: