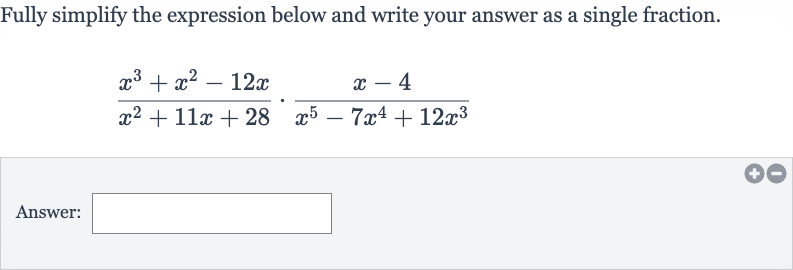
Fully simplify the expression below and write your answer as a single fraction. (x^(3)+x^(2)-12 x)/(x^(2)+11 x+28)*(x-4)/(x^(5)-7x^(4)+12x^(3)) Answer:

Question

Fully simplify the expression below and write your answer as a single fraction.  (x^(3)+x^(2)-12 x)/(x^(2)+11 x+28)*(x-4)/(x^(5)-7x^(4)+12x^(3)) Answer:

Bytelearn · Accepted Answer

Factor Numerator and Denominator: Factor the numerator and the denominator of the first fraction. The numerator x^3 + x^2 - 12x can be factored by taking out the common factor x: x(x^2 + x - 12) Now, factor the quadratic x^2 + x - 12: x(x + 4)(x - 3) The denominator x^2 + 11x + 28 can be factored into: (x + 4)(x + 7) So the first fraction becomes: x(x + 4)(x - 3) / (x + 4)(x + 7)Cancel Common Factors: Cancel out the common factors in the first fraction. The (x + 4) term is present in both the numerator and the denominator, so they cancel each other out: x(x - 3) / (x + 7)Factor Denominator: Factor the denominator of the second fraction. The denominator x^5 - 7x^4 + 12x^3 can be factored by taking out the common factor x^3: x^3(x^2 - 7x + 12) Now, factor the quadratic x^2 - 7x + 12: x^3(x - 3)(x - 4) So the second fraction becomes: (x - 4) / x^3(x - 3)(x - 4)Cancel Common Factors: Cancel out the common factors in the second fraction. The (x - 4) term is present in both the numerator and the denominator, so they cancel each other out: 1 / x^3(x - 3)Multiply Simplified Fractions: Multiply the simplified first fraction by the simplified second fraction. (x(x - 3) / (x + 7)) * (1 / x^3(x - 3)) Now, cancel out the common (x - 3) term: x / (x + 7) * 1 / x^3Combine Fractions: Simplify the expression by combining the fractions. x / (x + 7) * 1 / x^3 can be simplified by multiplying the numerators and denominators: (x * 1) / ((x + 7) * x^3) This simplifies to: x / (x^4 + 7x^3)Check Further Simplification: Check for any further simplification. There are no common factors left to cancel, and the expression is as simplified as it can be.

Fully simplify the expression below and write your answer as a single fraction. $\newline$ $\frac{x^{3}+x^{2}-12 x}{x^{2}+11 x+28} \cdot \frac{x-4}{x^{5}-7 x^{4}+12 x^{3}}$ $\newline$ Answer:

Full solution

More problems from Multiplication with rational exponents

Related topics

Fully simplify the expression below and write your answer as a single fraction.\newlinex3+x2−12xx2+11x+28⋅x−4x5−7x4+12x3 \frac{x^{3}+x^{2}-12 x}{x^{2}+11 x+28} \cdot \frac{x-4}{x^{5}-7 x^{4}+12 x^{3}} x2+11x+28x3+x2−12x​⋅x5−7x4+12x3x−4​\newlineAnswer:

Fully simplify the expression below and write your answer as a single fraction. $\newline$ $\frac{x^{3}+x^{2}-12 x}{x^{2}+11 x+28} \cdot \frac{x-4}{x^{5}-7 x^{4}+12 x^{3}}$ $\newline$ Answer: