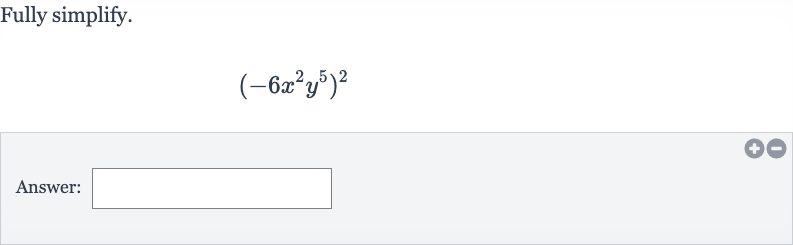AI tutor
Full solution
Q. Fully simplify.Answer:
- Identify base and exponent: Identify the base and the exponent in .In , the base is and the exponent is .
- Apply power of product rule: Apply the power of a product rule, which states that , to the base .
- Calculate each part separately: Calculate each part separately. because the square of a negative number is positive. because of the power of a power rule, which states that . for the same reason.
- Combine results: Combine the results from Step .
- Write final simplified expression: Write the final simplified expression.The simplified form is .
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help