AI tutor
Full solution
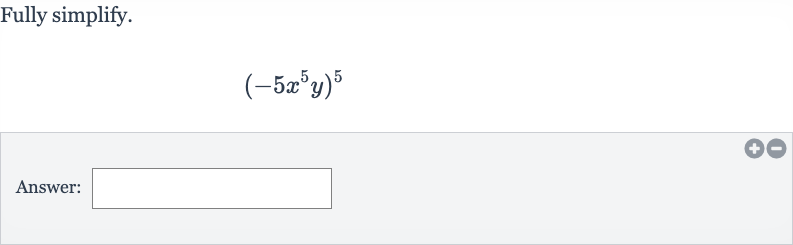
Q. Fully simplify.Answer:
- Apply Power Rule: To simplify the expression , we need to apply the power of a power rule, which states that for any real number and integers and .
- Raise Factors to Fifth Power: Applying the power of a power rule to the given expression, we raise each factor inside the parentheses to the fifth power: , , and .
- Calculate Each Part: Calculating each part separately, we get: (since multiplied by itself times is ), (multiplying the exponents), (since it's already in the correct form).
- Combine Results: Combining these results, we get the fully simplified expression:
More problems from Multiply and divide rational expressions
QuestionGet tutor help