AI tutor
Full solution
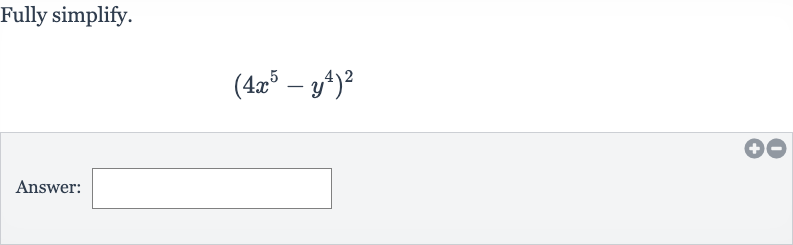
Q. Fully simplify.Answer:
- Apply Binomial Expansion Formula: To simplify the expression is and is .
- Square : First, we square the term to get .
- Square : Next, we square the term to get .
- Multiply and Double: Then, we multiply the two terms together and double them to get the middle term of the binomial expansion, which is .
- Combine All Terms: Now, we combine all the terms to get the fully simplified expression: .
More problems from Find trigonometric ratios using reference angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help