AI tutor
Full solution
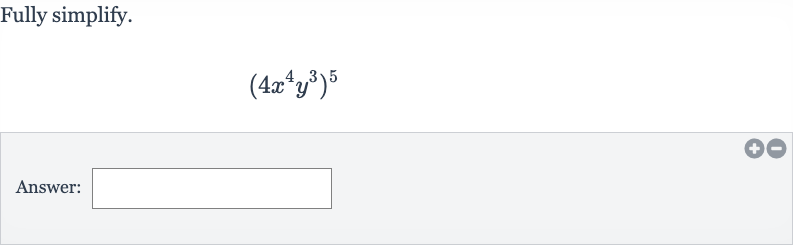
Q. Fully simplify.Answer:
- Identify base and exponent: Identify the base and the exponent in the expression 4x^{4}y^{3})^{5}\. In \$4x^{4}y^{3})^{5}\, the base is \$4x^{4}y^{3} and the exponent is .
- Apply power of product rule: Apply the power of a product rule, which states that , to the expression.(\(4x^{}y^{})^{} = ^ \times (x^{})^ \times (y^{})^
- Calculate powers separately: Calculate the powers separately.
- Combine results for final expression: Combine the results from Step to get the final simplified expression.
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help