AI tutor
Full solution
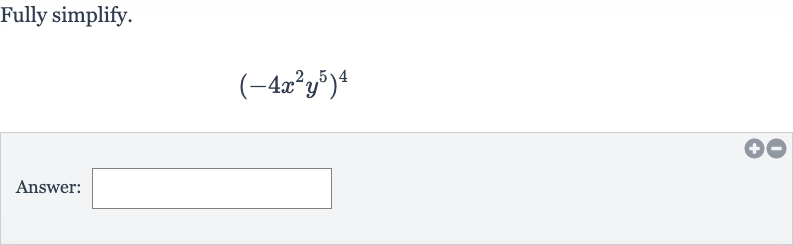
Q. Fully simplify.Answer:
- Identify base and exponents: Identify the base and the exponents in .In , the base is and the exponent is .
- Apply power rule: Apply the power rule to the expression. can be written as .
- Calculate each part: Calculate each part separately.First, because a negative number raised to an even power is positive.Second, because of the power of a power rule, which states that .Third, for the same reason.
- Combine results: Combine the results from the previous step. The expression simplifies to .
- Write final expression: Write the final simplified expression.The fully simplified form of is .
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help