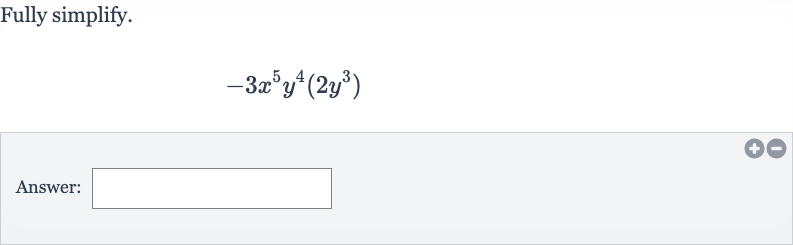AI tutor
Full solution
Q. Fully simplify.Answer:
- Identify Terms: Identify the terms to be multiplied in the expression . We have a constant , a term with , and two terms with and .
- Multiply Constants and Like Terms: Multiply the constants and the like terms separately.First, multiply the constants and to get .Then, since the bases are the same for the terms, add the exponents and to get .
- Combine Results: Combine the results from the previous step.We have from the constants, from the term, and from the terms.So, the expression becomes .
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help