AI tutor
Full solution
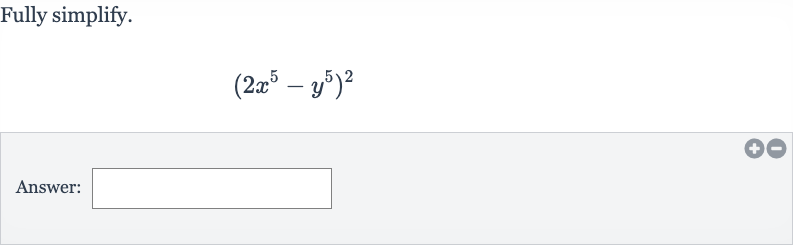
Q. Fully simplify.Answer:
- Recognize Structure: Recognize the structure of the expression.The given expression is a binomial raised to the second power. This can be expanded using the formula , where and .
- Apply Formula: Apply the binomial square formula.Using the formula from Step , we expand to get .
- Calculate Terms: Calculate each term separately.First term: ^ = x^{} *^ = x^{}\)Second term: and we just multiply the and terms)\)Third term: ^ = y^{} since \(y^5^ = y^{}\)
- Combine Simplified Expression: Combine the terms to get the final simplified expression.The fully simplified form of the expression is
More problems from Find trigonometric ratios using reference angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help