AI tutor
Full solution
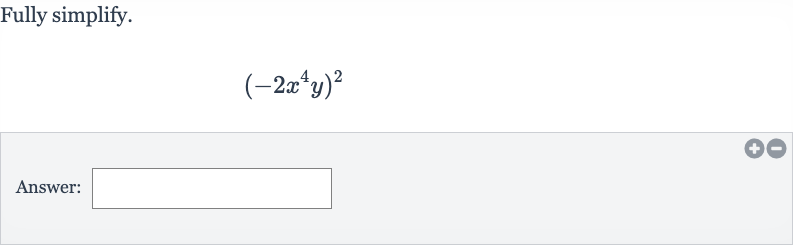
Q. Fully simplify.Answer:
- Identify base and exponent: Identify the base and the exponent in .In , the base is and the exponent is .
- Apply power of product rule: Apply the power of a product rule, which states that , to the base and the exponent.(\(-2x^{}y)^{} = ()^ \times (x^{})^ \times y^
- Simplify each term: Simplify each term separately. because the square of a negative number is positive. because of the power of a power rule, which states that . remains as it is because there is no exponent to apply to it.
- Multiply simplified terms: Multiply the simplified terms together to get the final answer.
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help