Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

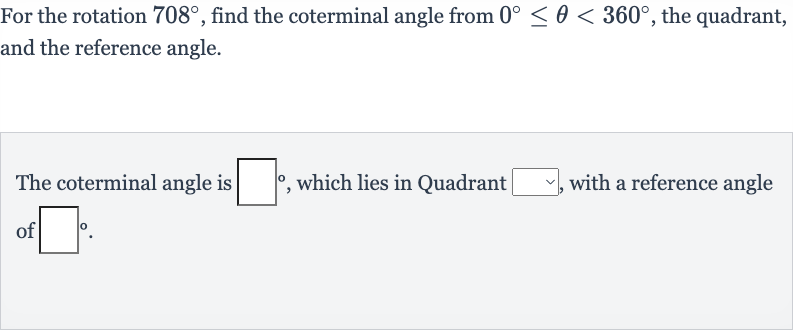
For the rotation 708^(@), find the coterminal angle from 0^(@) <= theta < 360^(@), the quadrant, and the reference angle. The coterminal angle is ◻^(@), which lies in Quadrant ◻, with a reference angle of ◻^(@).

For the rotation 708∘ 708^{\circ} , find the coterminal angle from 0∘≤θ<360∘ 0^{\circ} \leq \theta<360^{\circ} , the quadrant, and the reference angle.\newlineThe coterminal angle is □∘ \square^{\circ} , which lies in Quadrant □ \square , with a reference angle of □∘ \square^{\circ} .

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Transformations of quadratic functionsright chevron icon

Full solution

Q. For the rotation 708∘ 708^{\circ} , find the coterminal angle from 0∘≤θ<360∘ 0^{\circ} \leq \theta<360^{\circ} , the quadrant, and the reference angle.\newlineThe coterminal angle is □∘ \square^{\circ} , which lies in Quadrant □ \square , with a reference angle of □∘ \square^{\circ} .
  1. Subtract 360360 from 708708: To find the coterminal angle between 00 and 360360 degrees, subtract multiples of 360360 from 708708 until the result is within the desired range.\newlineCalculation: 708−360=348708 - 360 = 348.
  2. Identify coterminal angle: Since 348348 is less than 360360 and greater than 00, it is the coterminal angle we are looking for.
  3. Determine quadrant: To determine the quadrant, observe that 348348 degrees is between 270270 and 360360 degrees, which places it in Quadrant IV.
  4. Find reference angle: To find the reference angle, subtract the coterminal angle from 360360 degrees.\newlineCalculation: 360−348=12360 - 348 = 12 degrees.

More problems from Transformations of quadratic functions

Question
Solve by completing the square.\newlinem2−10m−29=0m^2 - 10m - 29 = 0\newlineWrite your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.\newline`m` = ____ or `m` = _____
Get tutor helpright-arrow

Posted 1 month ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 5 5 units up of f(x)=x2 f(x)=x^2 .\newlineWrite your answer in the form a(x–h)2+k a(x–h)^2+k , where a a , h h , and k k are integers.\newlineg(x)= g(x)= ____
Get tutor helpright-arrow

Posted 1 month ago

Question
What is the range of this quadratic function?\newliney=x2−4x+4y = x^2 - 4x + 4\newlineChoices:\newline{y∣y≥2}\left\{y \mid y \geq 2\right\}\newline{y∣y≤0}\left\{y \mid y \leq 0\right\}\newline{y∣y≥0}\left\{y \mid y \geq 0\right\}\newlineall real numbers\text{all real numbers}
Get tutor helpright-arrow

Posted 1 month ago

Question
Write the equation of the parabola that passes through the points (1,0)(1,0), (2,0)(2,0), and (3,–16)(3,\text{–}16). Write your answer in the form y=a(x–p)(x–q)y = a(x – p)(x – q), where aa, pp, and qq are integers, decimals, or simplified fractions.\newline______
Get tutor helpright-arrow

Posted 1 month ago

Question
Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.\newlinef2+8f+_____f^2 + 8f + \_\_\_\_\_
Get tutor helpright-arrow

Posted 1 month ago

Question
Solve for h h .\newlineh2+39h=0 h^2 + 39h = 0 \newline\newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.\newlineh= h = ____\newline
Get tutor helpright-arrow

Posted 1 month ago

Question
Write a quadratic function with zeros −9-9 and −7-7.\newlineWrite your answer using the variable xx and in standard form with a leading coefficient of 11.\newlinef(x)=_____f(x) = \_\_\_\_\_
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the equation of the axis of symmetry for the parabola y=x2y = x^2. \newlineSimplify any numbers and write them as proper fractions, improper fractions, or integers.\newline‾\underline{\hspace{3cm}}
Get tutor helpright-arrow

Posted 2 months ago

Question
Find g(x)g(x), where g(x)g(x) is the translation 88 units up of f(x)=x2f(x) = x^2.\newlineWrite your answer in the form a(x–h)2+ka(x – h)^2 + k, where aa, hh, and kk are integers.\newlineg(x)=g(x) = ______\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve for xx.\newlinex2=1x^2 = 1\newline\newlineWrite your answer in simplified, rationalized form.\newlinex=x = ______ or x=x = ______\newline
Get tutor helpright-arrow

Posted 2 months ago

View all (75)