Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

For the function f(x)=root(3)((4x)), find f^(-1)(x). f^(-1)(x)=((x)/(4))^(3) f^(-1)(x)=(4x)^(3) f^(-1)(x)=(x^(3))/(4) f^(-1)(x)=4x^(3)

For the function f(x)=(4x)3 f(x)=\sqrt[3]{(4 x)} , find f−1(x) f^{-1}(x) .\newlinef−1(x)=(x4)3 f^{-1}(x)=\left(\frac{x}{4}\right)^{3} \newlinef−1(x)=(4x)3 f^{-1}(x)=(4 x)^{3} \newlinef−1(x)=x34 f^{-1}(x)=\frac{x^{3}}{4} \newlinef−1(x)=4x3 f^{-1}(x)=4 x^{3}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Simplify the product of two radical expressions having same variableright chevron icon

Full solution

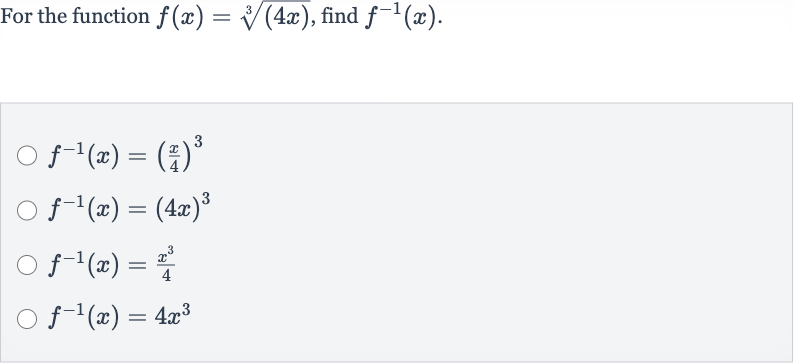
Q. For the function f(x)=(4x)3 f(x)=\sqrt[3]{(4 x)} , find f−1(x) f^{-1}(x) .\newlinef−1(x)=(x4)3 f^{-1}(x)=\left(\frac{x}{4}\right)^{3} \newlinef−1(x)=(4x)3 f^{-1}(x)=(4 x)^{3} \newlinef−1(x)=x34 f^{-1}(x)=\frac{x^{3}}{4} \newlinef−1(x)=4x3 f^{-1}(x)=4 x^{3}
  1. Write function as yy: To find the inverse function, we first write the function as y=4x3y = \sqrt[3]{4x}.
  2. Express cube root as exponent: Next, we express the cube root as an exponent: y=(4x)13y = (4x)^{\frac{1}{3}}.
  3. Swap xx and yy: To find the inverse, we swap xx and yy, so we get x=(4y)13x = (4y)^{\frac{1}{3}}.
  4. Cube both sides: Now we need to solve for yy. To do this, we cube both sides of the equation to get rid of the cube root: x3=4yx^3 = 4y.
  5. Isolate yy: Divide both sides by 44 to isolate yy: y=x34y = \frac{x^3}{4}.
  6. Find inverse function: Now we have the inverse function, which we denote as f−1(x)f^{-1}(x): f−1(x)=x34f^{-1}(x) = \frac{x^3}{4}.

More problems from Simplify the product of two radical expressions having same variable

Question
Find the real-number root. \newline16\sqrt{16}\newline\newlineWrite your answer in simplified form. \newline____\_\_\_\_
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the real-number root. \newline916\sqrt{\frac{9}{16}}\newlineSimplify your answer and write it as a decimal or as a proper or improper fraction.\newline_____\_\_\_\_\_
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the real-number root using a calculator. Round your answer to the nearest thousandth. \newline`\sqrt{957} `\newline _______
Get tutor helpright-arrow

Posted 2 months ago

Question
Multiply. Write your answer in simplest form. \newline273×42\sqrt{273} \times \sqrt{42}\newline______
Get tutor helpright-arrow

Posted 1 month ago

Question
Simplify. \newline634\sqrt{\frac{63}{4}}\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Simplify. Rationalize the denominator.\newline−49−2\frac{-4}{9 - \sqrt{2}}\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve for z z .\newline16=z 16 = \sqrt{z} \newlinez= z = _____
Get tutor helpright-arrow

Posted 2 months ago

Question
Simplify the radical expression. 14x14 \sqrt{14x^{14}} Write your answer in the form A A , B \sqrt{B} , or AB A\sqrt{B} , where A A and B B are constants or expressions in x x . Use at most one radical in your answer, and at most one absolute value symbol in your expression for A A . ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Simplify the radical expression.\newline12x12\sqrt{12x^{12}}\newlineWrite your answer in the form AA, B\sqrt{B}, or ABA\sqrt{B}, where AA and BB are constants or expressions in xx. Use at most one radical in your answer, and at most one absolute value symbol in your expression for AA.\newline‾\underline{\hspace{3cm}}
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the value of sin⁡(5π6)? \sin \left(\frac{5 \pi}{6}\right) ? \newlineChoose 11 answer:\newline(A) −32 -\frac{\sqrt{3}}{2} \newline(B) −22 -\frac{\sqrt{2}}{2} \newline(C) 12 \frac{1}{2} \newline(D) 150150
Get tutor helpright-arrow

Posted 4 months ago

View all (27)