AI tutor
Full solution
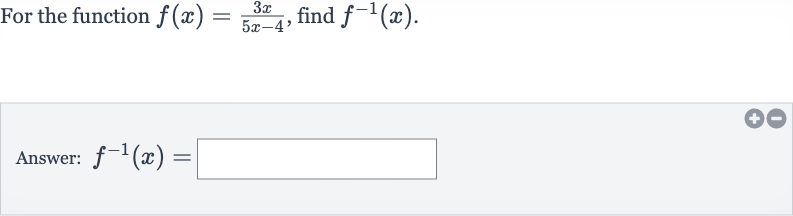
Q. For the function , find .Answer:
- Define Function: To find the inverse function, , we need to switch the roles of and in the original function and then solve for .
Let , so we have:
Now switch and : - Switch Roles: Next, we need to solve for . To do this, we'll multiply both sides of the equation by to get rid of the fraction.
- Eliminate Fraction: Now, we want to get all the terms involving on one side of the equation and the constant term on the other side.
- Combine Terms: Factor out from the left side of the equation.
- Factor Out: Now, divide both sides by to solve for .
- Solve for y: We have found the inverse function. So, is:
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help