AI tutor
Full solution
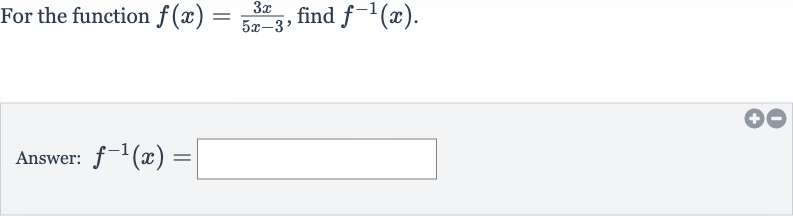
Q. For the function , find .Answer:
- Rewrite with y: To find the inverse function, , we need to switch the roles of and in the original function and then solve for . Let's start by rewriting the function with instead of :
- Switch x and y: Now, switch x and y to find the inverse:
- Multiply by : Next, we need to solve for . To do this, we'll multiply both sides of the equation by to get rid of the fraction:
- Distribute : Distribute on the left side of the equation:
- Move term: Now, we want to get all terms containing on one side of the equation and the constant term on the other side. Let's move the term to the left side by subtracting from both sides:
- Factor out : Factor out from the left side of the equation:
- Divide by : Now, divide both sides by to solve for :
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help