AI tutor
Full solution
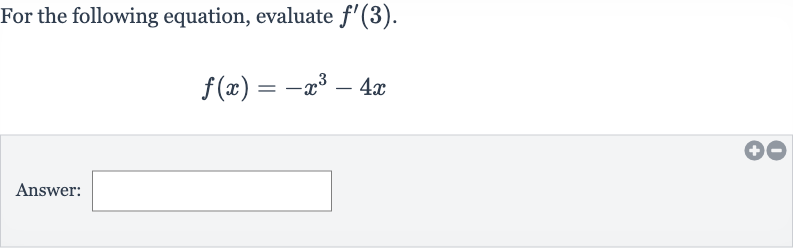
Q. For the following equation, evaluate .Answer:
- Identify Function and Point: Identify the function and the point at which the derivative is to be evaluated.We are given the function and we need to find the derivative of this function at .
- Calculate Derivative of Function: Calculate the derivative of the function . To find , we need to differentiate with respect to . Using the power rule, the derivative of is , and the derivative of is . So,
- Evaluate Derivative at : Evaluate the derivative at . Substitute into the derivative to find .
More problems from Find the vertex of the transformed function
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help