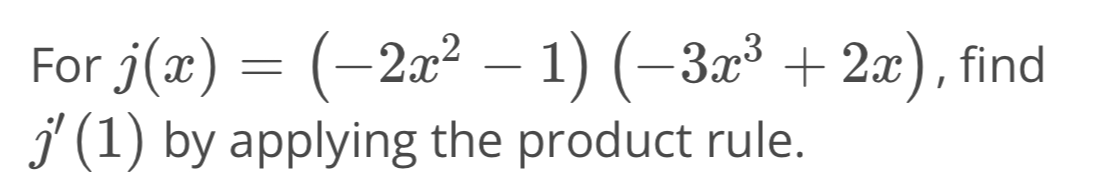For j(x)=(-2x^(2)-1)(-3x^(3)+2x), find j^(')(1) by applying the product rule.

Question

For  j(x)=(-2x^(2)-1)(-3x^(3)+2x), find  j^(')(1) by applying the product rule.

Bytelearn · Accepted Answer

Apply Product Rule: Apply the product rule to find the derivative of j(x). The product rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. So, if we have two functions u(x) and v(x), then the derivative of their product u(x)v(x) is given by u'(x)v(x) + u(x)v'(x). Let's define u(x) = -2x^2 - 1 and v(x) = -3x^3 + 2x.Find Derivative of u(x): Find the derivative of u(x) = -2x^2 - 1. The derivative of -2x^2 with respect to x is -4x, and the derivative of a constant (-1) is 0. So, u'(x) = -4x + 0, which simplifies to u'(x) = -4x.Find Derivative of v(x): Find the derivative of v(x) = -3x^3 + 2x. The derivative of -3x^3 with respect to x is -9x^2, and the derivative of 2x is 2. So, v'(x) = -9x^2 + 2.Apply Product Rule with Derivatives: Apply the product rule using the derivatives from steps 2 and 3. According to the product rule, j'(x) = u'(x)v(x) + u(x)v'(x). Substitute the derivatives and original functions into this formula: j'(x) = (-4x)(-3x^3 + 2x) + (-2x^2 - 1)(-9x^2 + 2).Simplify j'(x): Simplify the expression for j'(x). j'(x) = (12x^4 - 8x^2) + (18x^4 - 2x^2 - 9x^2 + 2). Combine like terms: j'(x) = 12x^4 - 8x^2 + 18x^4 - 11x^2 + 2. j'(x) = 30x^4 - 19x^2 + 2.Evaluate j'(x): Evaluate j'(x) at x = 1. Substitute x = 1 into the derivative: j'(1) = 30(1)^4 - 19(1)^2 + 2. Simplify the expression: j'(1) = 30 - 19 + 2. j'(1) = 13.

For $j(x)=\left(-2 x^{2}-1\right)\left(-3 x^{3}+2 x\right)$ , find $j^{\prime}(1)$ by applying the product rule.

Full solution

More problems from Multiplication with rational exponents

Related topics

For j(x)=(−2x2−1)(−3x3+2x) j(x)=\left(-2 x^{2}-1\right)\left(-3 x^{3}+2 x\right) j(x)=(−2x2−1)(−3x3+2x), find j′(1) j^{\prime}(1) j′(1) by applying the product rule.

For $j(x)=\left(-2 x^{2}-1\right)\left(-3 x^{3}+2 x\right)$ , find $j^{\prime}(1)$ by applying the product rule.