Find the zeros of the function $f(x)=x^{2}-8.4 x+12$ . Round values to the nearest hundredth (if necessary). $\newline$ Answer: $x=$

View step-by-step help

Home

Math Problems

Algebra 2

Find trigonometric functions using a calculator

Full solution

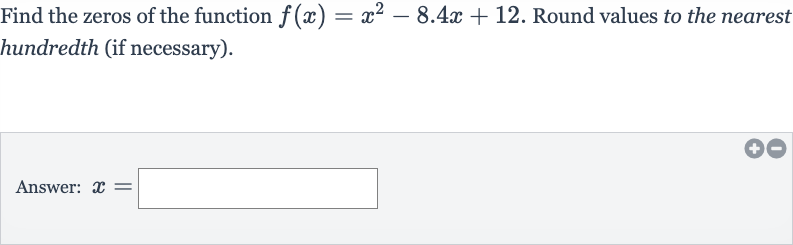
Q. Find the zeros of the function

f(x)=x^{2}-8.4 x+12

. Round values to the nearest hundredth (if necessary).

\newline

Answer:

x=

Identify equation type and method: Identify the type of equation and the method to find its zeros. $\newline$ The given function $f(x) = x^2 - 8.4x + 12$ is a quadratic equation in the standard form $f(x) = ax^2 + bx + c$ , where $a = 1$ , $b = -8.4$ , and $c = 12$ . To find the zeros of the quadratic equation, we can use the quadratic formula $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$ .
Apply quadratic formula: Apply the quadratic formula to find the zeros. $\newline$ Using the values $a = 1$ , $b = -8.4$ , and $c = 12$ , we substitute them into the quadratic formula: $\newline$ $x = \frac{-(-8.4) \pm \sqrt{(-8.4)^2 - 4 \cdot 1 \cdot 12}}{2 \cdot 1}$ $\newline$ $x = \frac{8.4 \pm \sqrt{70.56 - 48}}{2}$ $\newline$ $x = \frac{8.4 \pm \sqrt{22.56}}{2}$
Calculate discriminant and square root: Calculate the discriminant and the square root. $\newline$ The discriminant is the part under the square root in the quadratic formula, which is $22.56$ in this case. Taking the square root of $22.56$ gives us: $\newline$ $\sqrt{22.56} \approx 4.75$
Find possible values for x: Find the two possible values for x. $\newline$ Now we have two possible solutions for x: $\newline$ $x = \frac{8.4 + 4.75}{2}$ $\newline$ $x = \frac{8.4 - 4.75}{2}$
Calculate zeros of function: Calculate the zeros of the function. $\newline$ First zero: $\newline$ $x = \frac{8.4 + 4.75}{2}$ $\newline$ $x = \frac{13.15}{2}$ $\newline$ $x \approx 6.575$ $\newline$ Round to the nearest hundredth: $\newline$ $x \approx 6.58$ $\newline$ Second zero: $\newline$ $x = \frac{8.4 - 4.75}{2}$ $\newline$ $x = \frac{3.65}{2}$ $\newline$ $x \approx 1.825$ $\newline$ Round to the nearest hundredth: $\newline$ $x \approx 1.83$