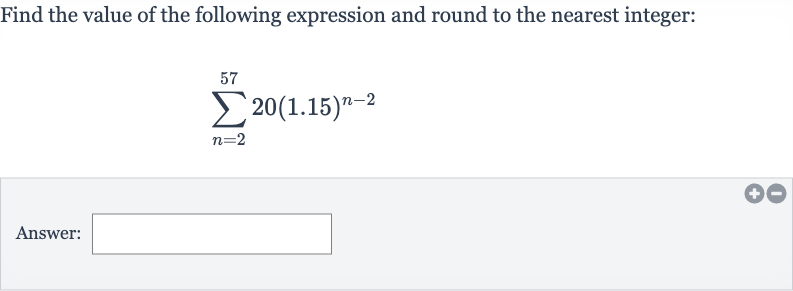
Find the value of the following expression and round to the nearest integer: sum_(n=2)^(57)20(1.15)^(n-2) Answer:

Question

Find the value of the following expression and round to the nearest integer:  sum_(n=2)^(57)20(1.15)^(n-2) Answer:

Bytelearn · Accepted Answer

Given geometric series: We are given a geometric series with the first term a = 20(1.15)^(2-2) = 20 and a common ratio r = 1.15. The sum of a finite geometric series can be found using the formula S_n = a(1 - r^n) / (1 - r), where n is the number of terms.Determine number of terms: First, we need to determine the number of terms in the series. Since the series starts at n=2 and goes to n=57, the number of terms is 57 - 2 + 1 = 56.Apply sum formula: Now we can apply the formula for the sum of a geometric series: S_n = a(1 - r^n) / (1 - r). Plugging in the values, we get S_56 = 20(1 - 1.15^56) / (1 - 1.15).Calculate numerator: Let's calculate the numerator of the fraction: 1 - 1.15^56. Using a calculator, we find that 1.15^56 ≈ 142.061.Calculate denominator: Subtracting this from 1 gives us 1 - 142.061 ≈ -141.061.Divide numerator by denominator: Now we calculate the denominator of the fraction: 1 - 1.15 = -0.15.Multiply by first term: We can now divide the numerator by the denominator: -141.061 / -0.15 ≈ 940.407.Round to nearest integer: Multiplying this result by the first term of the series (20) gives us the sum of the series: 940.407 * 20 ≈ 18808.14.Finally, we round the result to the nearest integer: 18808.14 rounds to 18808.

Find the value of the following expression and round to the nearest integer: $\newline$ $\sum_{n=2}^{57} 20(1.15)^{n-2}$ $\newline$ Answer:

Full solution

More problems from Sum of finite series starts from 1

Related topics

Find the value of the following expression and round to the nearest integer:\newline∑n=25720(1.15)n−2 \sum_{n=2}^{57} 20(1.15)^{n-2} n=2∑57​20(1.15)n−2\newlineAnswer:

Find the value of the following expression and round to the nearest integer: $\newline$ $\sum_{n=2}^{57} 20(1.15)^{n-2}$ $\newline$ Answer: