Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the value of the following expression and round to the nearest integer: sum_(n=0)^(93)400(0.94)^(n+1) Answer:

Find the value of the following expression and round to the nearest integer:\newline∑n=093400(0.94)n+1 \sum_{n=0}^{93} 400(0.94)^{n+1} \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Find trigonometric functions using a calculatorright chevron icon

Full solution

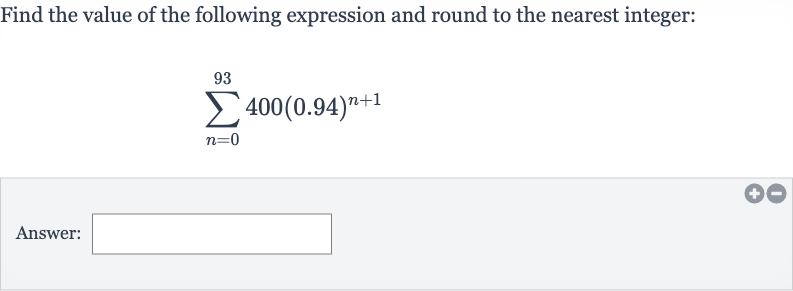
Q. Find the value of the following expression and round to the nearest integer:\newline∑n=093400(0.94)n+1 \sum_{n=0}^{93} 400(0.94)^{n+1} \newlineAnswer:
  1. Identify Geometric Series: The given expression is a geometric series where the first term a1a_1 is 400×0.94400 \times 0.94, the common ratio rr is 0.940.94, and the number of terms nn is 9494 (since we start counting from 00 up to 9393).
  2. Calculate Sum Formula: To find the sum of a geometric series, we use the formula S=a1×(1−rn)/(1−r)S = a_1 \times (1 - r^n) / (1 - r), where SS is the sum of the series.
  3. Calculate First Term: First, calculate the first term a1a_1: a1=400×0.94=376a_1 = 400 \times 0.94 = 376.
  4. Calculate rnr^n: Next, calculate rnr^n: rn=0.9494r^n = 0.94^{94}. This calculation might be difficult to do exactly without a calculator, but we can estimate it to be very small since 0.940.94 is less than 11 and raised to a high power.
  5. Plug Values into Formula: Now, we can plug the values into the sum formula: S=376×(1−0.9494)/(1−0.94)S = 376 \times (1 - 0.94^{94}) / (1 - 0.94).
  6. Approximate rnr^n: Since 0.94940.94^{94} is very small, we can approximate it to 00 for the purpose of this calculation. Therefore, the formula simplifies to S≈3761−0.94S \approx \frac{376}{1 - 0.94}.
  7. Calculate Denominator: Calculate the denominator: 1−0.94=0.061 - 0.94 = 0.06.
  8. Divide First Term: Now, divide the first term by the denominator: S≈3760.06S \approx \frac{376}{0.06}.
  9. Perform Division: Perform the division: S≈3760.06≈6266.67S \approx \frac{376}{0.06} \approx 6266.67.
  10. Round Final Result: Finally, round the result to the nearest integer: S≈6267S \approx 6267.

More problems from Find trigonometric functions using a calculator

Question
Find all solutions with 0∘≤θ≤180∘0^\circ \leq \theta \leq 180^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecos⁡(θ)=−1\cos(\theta) = -1\newline‾∘\underline{\hspace{2em}}^\circ
Get tutor helpright-arrow

Posted 7 months ago

Question
Kimi's school is 1515 kilometers west of her house and 88 kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?\newline_____\_\_\_\_\_ kilometers
Get tutor helpright-arrow

Posted 7 months ago

Question
Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.\newlinecos⁡35∘=\cos 35^\circ = __
Get tutor helpright-arrow

Posted 7 months ago

Question
Find all solutions with −90∘≤θ≤90∘-90^\circ \leq \theta \leq 90^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecsc⁡(θ)=−1\csc(\theta) = -1\newline____ ∘\_\_\_\_\,^\circ
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecot⁡30∘=\cot 30^\circ = ______
Get tutor helpright-arrow

Posted 7 months ago

Question
The terminal side of an angle θ\theta in standard position intersects the unit circle at (8485,1385)(\frac{84}{85}, \frac{13}{85}). What is cos⁡(θ)\cos(\theta)?\newlineWrite your answer in simplified, rationalized form.\newline______
Get tutor helpright-arrow

Posted 7 months ago

Question
−90∘<θ<90∘-90^\circ < \theta < 90^\circ. Find the value of θ\theta in degrees.\newlinetan⁡(θ)=0\tan(\theta) = 0\newlineWrite your answer in simplified, rationalized form. Do not round.\newlineθ=\theta = ____∘^\circ\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecsc⁡60∘=\csc 60^\circ = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
θ\theta is an acute angle. Find the value of θ\theta in degrees.\newlinesec⁡(θ)=2\sec(\theta) = \sqrt{2}\newlineθ=\theta = ____°\degree
Get tutor helpright-arrow

Posted 7 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecos⁡90∘=\cos 90^\circ = ____
Get tutor helpright-arrow

Posted 8 months ago

View all (217)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant