Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the sum of the first 9 terms of the following series, to the nearest integer. 2,(5)/(2),(25)/(8),dots Answer:

Find the sum of the first 99 terms of the following series, to the nearest integer.\newline2,52,258,… 2, \frac{5}{2}, \frac{25}{8}, \ldots \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Multiplication with rational exponentsright chevron icon

Full solution

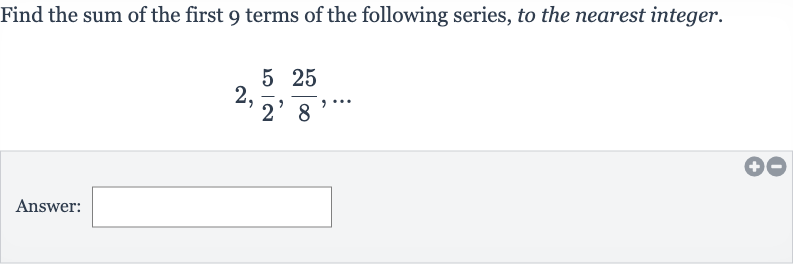
Q. Find the sum of the first 99 terms of the following series, to the nearest integer.\newline2,52,258,… 2, \frac{5}{2}, \frac{25}{8}, \ldots \newlineAnswer:
  1. Identify pattern: Identify the pattern of the series.\newlineThe given series is 2,52,258,…2, \frac{5}{2}, \frac{25}{8}, \ldots which looks like a geometric series. To confirm this, we need to find the common ratio by dividing the second term by the first term and the third term by the second term.\newlineCommon ratio (r)=522=54(r) = \frac{\frac{5}{2}}{2} = \frac{5}{4}\newlineAnd, r=25852=258×25=54r = \frac{\frac{25}{8}}{\frac{5}{2}} = \frac{25}{8} \times \frac{2}{5} = \frac{5}{4}\newlineSince the common ratio is the same for these terms, we can confirm that this is a geometric series with a common ratio of 54\frac{5}{4}.
  2. Use formula for sum: Use the formula for the sum of the first nn terms of a geometric series.\newlineThe sum of the first nn terms of a geometric series is given by the formula:\newlineSn=a⋅(1−rn)/(1−r)S_n = a \cdot (1 - r^n) / (1 - r), where aa is the first term, rr is the common ratio, and nn is the number of terms.\newlineIn this case, a=2a = 2, r=5/4r = 5/4, and n=9n = 9.
  3. Substitute and calculate: Substitute the values into the formula and calculate the sum.\newlineS9=2×(1−(54)9)/(1−54)S_9 = 2 \times (1 - (\frac{5}{4})^9) / (1 - \frac{5}{4})\newlineSince 54\frac{5}{4} is greater than 11, the series is divergent, and we need to adjust the formula to account for this:\newlineS9=2×((54)9−1)/(54−1)S_9 = 2 \times ((\frac{5}{4})^9 - 1) / (\frac{5}{4} - 1)\newlineS9=2×((54)9−1)/(14)S_9 = 2 \times ((\frac{5}{4})^9 - 1) / (\frac{1}{4})\newlineNow, calculate (54)9(\frac{5}{4})^9:\newline(54)9=5949(\frac{5}{4})^9 = \frac{5^9}{4^9}
  4. Calculate 595^9 and 494^9: Calculate 595^9 and 494^9.\newline59=19531255^9 = 1953125\newline49=2621444^9 = 262144\newlineNow we can continue with the calculation of S9S_9:\newlineS9=2×(1953125262144−1)/(14)S_9 = 2 \times (\frac{1953125}{262144} - 1) / (\frac{1}{4})
  5. Simplify expression: Simplify the expression.\newlineS9=2×(1953125262144−262144262144)/(14)S_9 = 2 \times (\frac{1953125}{262144} - \frac{262144}{262144}) / (\frac{1}{4})\newlineS9=2×(1953125−262144)/262144/(14)S_9 = 2 \times (1953125 - 262144) / 262144 / (\frac{1}{4})\newlineS9=2×(1690981262144)×4S_9 = 2 \times (\frac{1690981}{262144}) \times 4\newlineS9=2×169098165536S_9 = 2 \times \frac{1690981}{65536}\newlineS9=338196265536S_9 = \frac{3381962}{65536}
  6. Divide for sum: Divide to find the sum to the nearest integer.\newlineS9≈338196265536S_9 \approx \frac{3381962}{65536}\newlineS9≈51.6S_9 \approx 51.6\newlineTo the nearest integer, the sum is approximately 5252.

More problems from Multiplication with rational exponents

Question
Simplify.\newline811281^{\frac{1}{2}}\newline_____________
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify.\newline(−32)1/5(-32)^{1/5}\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify. Assume all variables are positive.\newlinew43w73\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. Assume all variables are positive.\newline(2r13)8(2r^{\frac{1}{3}})^8\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. Assume all variables are positive.\newlinev74⋅v94v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify.\newline114⋅1141^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. \newline32(−1/5)32^{(-1/5)}
Get tutor helpright-arrow

Posted 7 months ago

Question
Simplify. Assume all variables are positive.\newlinew32w52\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify. Assume all variables are positive.\newline(27x)23(27x)^{\frac{2}{3}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 8 months ago

Question
Simplify. Assume all variables are positive.\newlinex14x114\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 7 months ago

View all (744)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant