Full solution
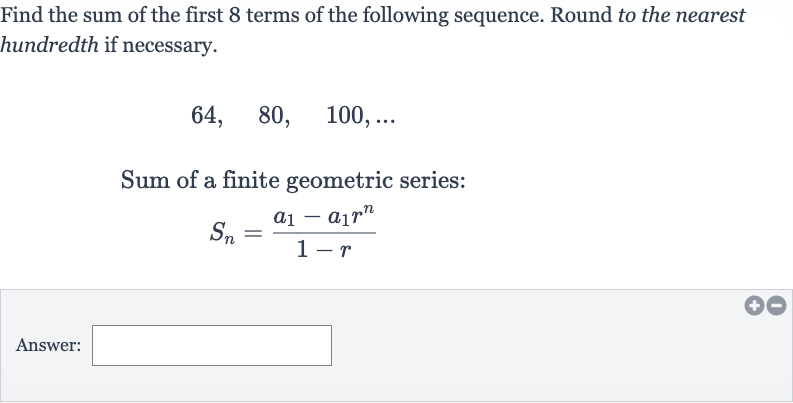
Q. Find the sum of the first terms of the following sequence. Round to the nearest hundredth if necessary.Sum of a finite geometric series:Answer:
- Identify sequence type: First, identify the type of sequence given. The sequence suggests that it is an arithmetic sequence because the difference between consecutive terms is constant.
- Determine common difference: Determine the common difference of the arithmetic sequence by subtracting the first term from the second term: .
- Use sum formula: Use the formula for the sum of the first terms of an arithmetic sequence: , where is the sum of the first terms, is the first term, and is the common difference.
- Plug values into formula: Plug the values into the formula to find the sum of the first terms: .
- Simplify expression: Simplify the expression: .
- Calculate sum: Calculate the sum: .