Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the sum of the first 25 terms in this geometric series:

8+6+4.5 dots
Choose 1 answer:
(A) 0.03
(B) 4.57
(c)
29.91
(D) 31.98

Find the sum of the first $25$ terms in this geometric series: $\newline$ $8+6+4.5 \ldots$ $\newline$ Choose $1$ answer: $\newline$ (A) $0$ . $03$ $\newline$ (B) $4$ . $57$ $\newline$ (C) $\mathbf{2 9 . 9 1}$ $\newline$ (D) $31$ . $98$

View step-by-step help

View step-by-step help

Find the sum of a finite geometric series

Full solution

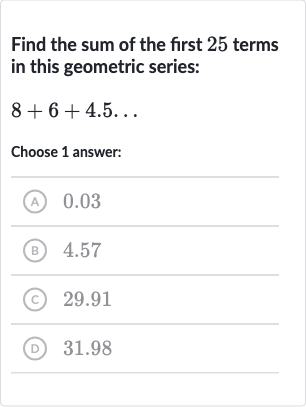
Q. Find the sum of the first

25

terms in this geometric series:

\newline

8+6+4.5 \ldots

\newline

Choose

1

answer:

\newline

(A)

0

.

03

\newline

(B)

4

.

57

\newline

(C)

\mathbf{2 9 . 9 1}

\newline

(D)

31

.

98

Identify first term: Identify the first term ( $a_1$ ) of the geometric series. $\newline$ The first term is given as $8$ .
Calculate common ratio: Identify the second term $a_2$ and calculate the common ratio $r$ . The second term is given as $6$ . To find the common ratio, divide the second term by the first term. $r = \frac{a_2}{a_1} = \frac{6}{8} = 0.75$
Use formula for sum: Use the formula for the sum of the first $n$ terms of a geometric series. $\newline$ The formula is: $\newline$ $S_n = \frac{a_1(1 - r^n)}{1 - r}$ $\newline$ We have: $\newline$ $a_1 = 8$ $\newline$ $r = 0.75$ $\newline$ $n = 25$
Substitute values and calculate: Substitute the values into the formula and calculate the sum. $\newline$ $S_{25} = \frac{8(1 - 0.75^{25})}{(1 - 0.75)}$ $\newline$ Calculate $0.75^{25}$ using a calculator. $\newline$ $0.75^{25} \approx 0.000316$
Continue calculation: Continue the calculation. $\newline$ $S_{25} = \frac{8(1 - 0.000316)}{1 - 0.75}$ $\newline$ $S_{25} = \frac{8(0.999684)}{0.25}$
Complete calculation: Complete the calculation. $\newline$ $S_{25} = 8 \times 0.999684 / 0.25$ $\newline$ $S_{25} = 7.997472 / 0.25$ $\newline$ $S_{25} = 31.989888$
Round the result: Round the result to two decimal places, as the answer choices are given in two decimal places. $\newline$ $S_{25} \approx 31.99$

More problems from Find the sum of a finite geometric series

Question

Find the sum of the finite arithmetic series.

\sum_{n=1}^{10} (7n+4)

\newline

Posted 2 months ago

Question

Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`

Posted 1 month ago

Question

Type the missing number in this sequence: `2, 4 8`, ______,`32`

Posted 2 months ago

Question

What kind of sequence is this?

2, 10, 50, 250, \ldots

Choices:Choices:

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 2 months ago

Question

What is the missing number in this pattern?

1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_

Posted 1 month ago

Question

Classify the series.

\sum_{n = 0}^{12} (n + 2)^3

\newline

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 1 month ago

Question

Find the first three partial sums of the series.

\newline

1 + 6 + 11 + 16 + 21 + 26 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 1 month ago

Question

Find the third partial sum of the series.

\newline

3 + 9 + 15 + 21 + 27 + 33 + \cdots

\newline

Write your answer as an integer or a fraction in simplest form.

\newline

S_3 =

Posted 1 month ago

Question

Find the first three partial sums of the series.

\newline

1 + 7 + 13 + 19 + 25 + 31 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 2 months ago

Question

Does the infinite geometric series converge or diverge?

\newline

1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots

\newline

\newline

\text{[A]converge}

\newline

\text{[B]diverge}

Posted 1 month ago