Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

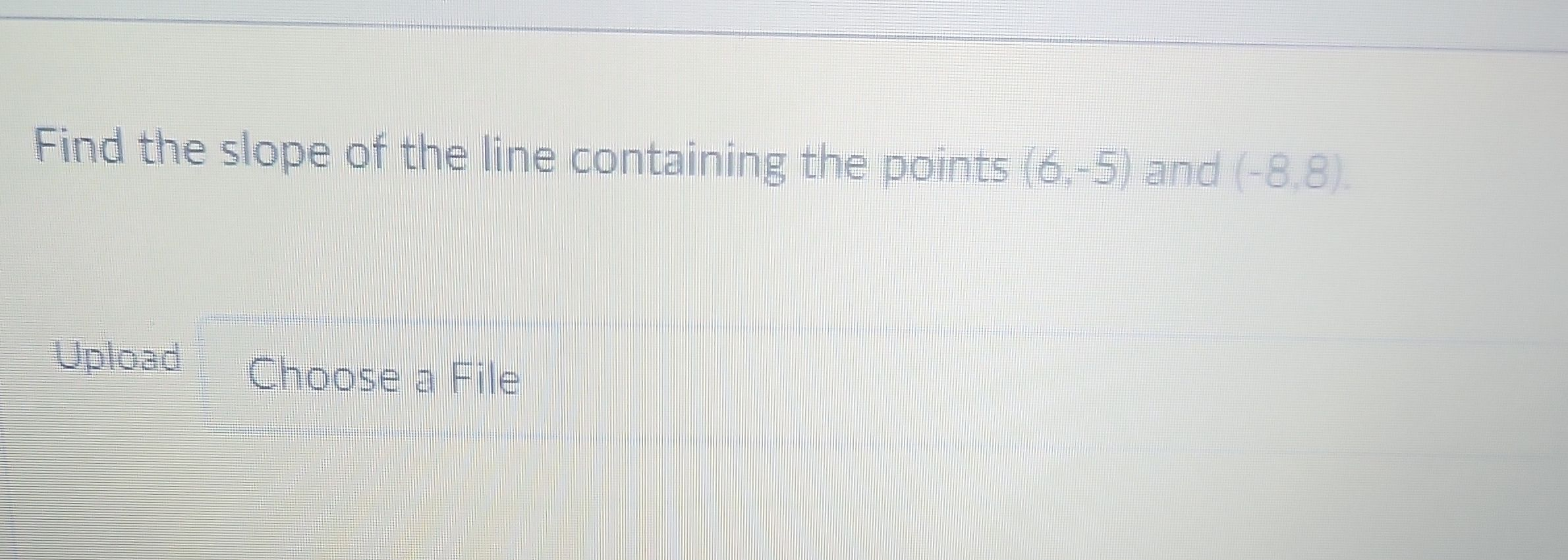
Find the slope of the line containing the points (6,-5) and (-8,8). ◻

Find the slope of the line containing the points (6,−5) (6,-5) and (−8,8) (-8,8) .\newline□\square

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Find a missing coordinate using sloperight chevron icon

Full solution

Q. Find the slope of the line containing the points (6,−5) (6,-5) and (−8,8) (-8,8) .\newline□\square
  1. Identify Points: Identify the given points.\newlineWe have two points: Point 11 (x1,y1)=(6,−5)(x_1, y_1) = (6, -5) and Point 22 (x2,y2)=(−8,8)(x_2, y_2) = (-8, 8).\newlineWe will use these points to calculate the slope of the line.
  2. Use Slope Formula: Use the slope formula.\newlineThe slope mm of a line passing through two points (x1,y1)(x_1, y_1) and (x2,y2)(x_2, y_2) is given by the formula:\newlinem=y2−y1x2−x1m = \frac{y_2 - y_1}{x_2 - x_1}
  3. Plug in Values: Plug in the values from the points into the slope formula.\newlinem=8−(−5)−8−6m = \frac{8 - (-5)}{-8 - 6}
  4. Simplify Numerator and Denominator: Simplify the numerator and the denominator.\newlinem=8+5−8−6m = \frac{8 + 5}{-8 - 6}\newlinem=13−14m = \frac{13}{-14}
  5. Simplify Fraction: Simplify the fraction to get the slope. \newlinem=−1314m = -\frac{13}{14}\newlineThis is the slope of the line containing the points (6,−5)(6, -5) and (−8,8)(-8, 8).

More problems from Find a missing coordinate using slope

Question
What is the slope of the line through (−2,−6)(-2,-6) and (2,2)(2,2)?\newlineChoose 11 answer:\newline(A) 12\frac{1}{2}\newline(B) −2-2\newline(C) 22\newline(D) −12-\frac{1}{2}
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the slope of the line through (−10,1)(-10,1) and (0,−4)(0,-4)? Choose 11 answer: \newline(A) 22 \newline(B) 12\frac{1}{2} \newline(C) −12-\frac{1}{2} \newline(D) −2-2
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the slope of the line through (−9,−6)(-9,-6) and (3,−9)(3,-9)? Choose 11 answer: \newline(A) −4-4 \newline(B) 14\frac{1}{4} \newline(C) 44 \newline(D) −14-\frac{1}{4}
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the slope of the line through \newline(−5,−10)(-5,-10) and \newline(−1,5)(-1,5)?\newlineChoose 11 answer:\newline(A) \newline154\frac{15}{4}\newline(B) \newline415\frac{4}{15}\newline(C) \newline−154-\frac{15}{4}\newline(D) \newline−415-\frac{4}{15}
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the slope of the line through (−1,8)(-1,8) and (3,−4)(3,-4)? Choose 11 answer: \newline(A) −13-\frac{1}{3} \newline(B) 13\frac{1}{3} \newline(C) 33 \newline(D) −3-3
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the slope of the line through (−4,2)(-4,2) and (3,−3)(3,-3)? Choose 11 answer: (A) 75\frac{7}{5} (B) −75-\frac{7}{5} (C) −57-\frac{5}{7} (D) 57\frac{5}{7}
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the slope of the line through (2,−2)(2,-2) and (9,3)(9,3)? \newlineChoose 11 answer:\newline(A) 57\frac{5}{7}\newline(B) −57-\frac{5}{7}\newline(C) 75\frac{7}{5}\newline(D) −75-\frac{7}{5}
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the slope of the line through (1,−1)(1,-1) and (5,−7)(5,-7)? Choose 11 answer: (A) −32-\frac{3}{2} (B) 32\frac{3}{2} (C) −23-\frac{2}{3} (D) 23\frac{2}{3}
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the slope of the line through (1,0)(1,0) and (3,8)(3,8)? Choose 11 answer: (A) −14-\frac{1}{4} (B) 44 (C) −4-4 (D) 14\frac{1}{4}
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the slope of the line through (−1,−7)(-1,-7) and (3,9)(3,9)?\newlineChoose 11 answer:\newline(A) 14\frac{1}{4}\newline(B) 44\newline(C) −14-\frac{1}{4}\newline(D) −4-4
Get tutor helpright-arrow

Posted 4 months ago

View all (97)