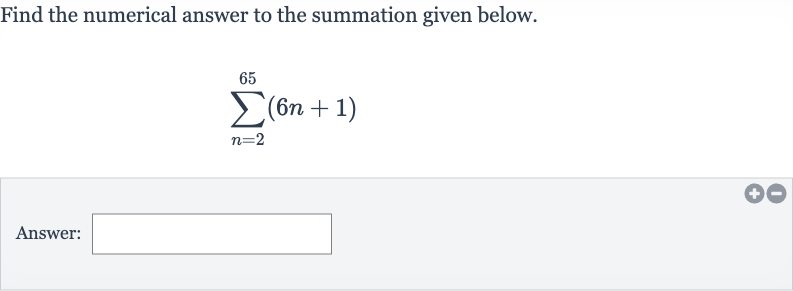
Find the numerical answer to the summation given below. sum_(n=2)^(65)(6n+1) Answer:

Question

Find the numerical answer to the summation given below.  sum_(n=2)^(65)(6n+1) Answer:

Bytelearn · Accepted Answer

Recognize Problem Split: Recognize that the summation of (6n+1) from n=2 to n=65 can be split into two separate summations: the summation of 6n and the summation of 1.Calculate Sum 6n: Calculate the summation of 6n from n=2 to n=65. This is an arithmetic series where each term increases by a constant difference (6). The sum of an arithmetic series can be found using the formula: S = n/2 * (a1 + an), where n is the number of terms, a1 is the first term, and an is the last term.Find Number of Terms: Find the number of terms in the series. Since we are summing from n=2 to n=65, there are 65 - 2 + 1 = 64 terms.Calculate First Term: Calculate the first term (a1) when n=2, which is 6*2+1 = 13 (not just 6*2 because we need to consider the +1 in the original expression).Calculate Last Term: Calculate the last term (an) when n=65, which is 6*65+1 = 391.Use Sum Formula: Use the arithmetic series sum formula to find the sum of 6n from n=2 to n=65. S = 64/2 * (13 + 391) S = 32 * 404 S = 12928Calculate Sum 1: Calculate the summation of 1 from n=2 to n=65. Since the sum of 1 added 64 times is simply 64, we can directly write this sum as 64.Add Results for Final Answer: Add the results from Step 6 and Step 7 to get the final answer. Total Sum = 12928 (sum of 6n) + 64 (sum of 1) Total Sum = 12992

Find the numerical answer to the summation given below. $\newline$ $\sum_{n=2}^{65}(6 n+1)$ $\newline$ Answer:

Full solution

More problems from Sum of finite series starts from 1

Related topics

Find the numerical answer to the summation given below.\newline∑n=265(6n+1) \sum_{n=2}^{65}(6 n+1) n=2∑65​(6n+1)\newlineAnswer:

Find the numerical answer to the summation given below. $\newline$ $\sum_{n=2}^{65}(6 n+1)$ $\newline$ Answer: